题目内容
3.Rt△ABC中,∠ACB=90°,AC=5,BC=12,则它的内切圆半径为2.分析 设AB、BC、AC与⊙O的切点分别为D、F、E;易证得四边形OECF是正方形;那么根据切线长定理可得:CE=CF=$\frac{1}{2}$(AC+BC-AB),由此可求出r的长.
解答 解:如图: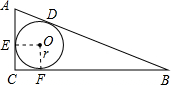
在Rt△ABC,∠C=90°,AC=5,BC=12,
根据勾股定理AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13,
四边形OECF中,OE=OF,∠OEC=∠OFC=∠C=90°,
∴四边形OECF是正方形,
由切线长定理,得:AD=AE,BD=BF,CE=CF,
∴CE=CF=$\frac{1}{2}$(AC+BC-AB),
即:r=$\frac{1}{2}$(5+12-13)=2.
故答案为:2.
点评 本题主要考查了直角三角形内切圆的性质及半径的求法.根据已知得出CE=CF=$\frac{1}{2}$(AC+BC-AB)是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8. 如图,Rt△ABC的斜边AB与⊙O相切于点B,直角顶点C在⊙O上,若AC=2$\sqrt{2}$,BC=4,则⊙O的半径是( )
如图,Rt△ABC的斜边AB与⊙O相切于点B,直角顶点C在⊙O上,若AC=2$\sqrt{2}$,BC=4,则⊙O的半径是( )
 如图,Rt△ABC的斜边AB与⊙O相切于点B,直角顶点C在⊙O上,若AC=2$\sqrt{2}$,BC=4,则⊙O的半径是( )
如图,Rt△ABC的斜边AB与⊙O相切于点B,直角顶点C在⊙O上,若AC=2$\sqrt{2}$,BC=4,则⊙O的半径是( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 2$\sqrt{6}$ |
15. 我们知道,将一个立方体沿某些棱剪开,可以得到它的平面展开图,请画出下面立方体的一种平面展开图,并分别把-3,-2,-1,1,2,3分别填入展开后的六个正方形内,且使原立方体相对面上的两数和为0.
我们知道,将一个立方体沿某些棱剪开,可以得到它的平面展开图,请画出下面立方体的一种平面展开图,并分别把-3,-2,-1,1,2,3分别填入展开后的六个正方形内,且使原立方体相对面上的两数和为0.
 我们知道,将一个立方体沿某些棱剪开,可以得到它的平面展开图,请画出下面立方体的一种平面展开图,并分别把-3,-2,-1,1,2,3分别填入展开后的六个正方形内,且使原立方体相对面上的两数和为0.
我们知道,将一个立方体沿某些棱剪开,可以得到它的平面展开图,请画出下面立方体的一种平面展开图,并分别把-3,-2,-1,1,2,3分别填入展开后的六个正方形内,且使原立方体相对面上的两数和为0.
13.在-2,-2$\frac{1}{2}$,0,2四个数中,最小的数是( )
| A. | -2 | B. | -2$\frac{1}{2}$ | C. | 0 | D. | 2 |
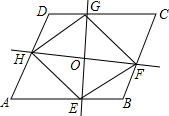 如图,过?ABCD中对角线的中点O作两条互相垂直的直线,分别交AB、BC、CD、DA于E、F、G、H,试判断四边形EFGH的形状并说明理由.
如图,过?ABCD中对角线的中点O作两条互相垂直的直线,分别交AB、BC、CD、DA于E、F、G、H,试判断四边形EFGH的形状并说明理由.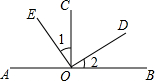 如图,点A,O,B在一条直线上,∠AOC=∠BOC,若∠1=∠2,则图中互余的角共有( )种.
如图,点A,O,B在一条直线上,∠AOC=∠BOC,若∠1=∠2,则图中互余的角共有( )种.