题目内容
1.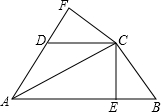 如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,(1)求证:BE=DF;
(2)若AB=21,AD=9,BC=CD=10,求AC的长.
分析 (1)根据HL证出两直角三角形全等即可;
(2)根据全等三角形性质推出AF=AE,DF=BE,设BE=x,则AE=21-x,DF=x,AF=9+x,得出方程21-x=9+x,求出BE,根据勾股定理求出CE即可.
解答 解(1)∵AC平分∠BAD,CE⊥AB,CF⊥AD,
∴CE=CF,△BCE与△DCF都是直角三角形,
在Rt△BEC和Rt△DFC中
$\left\{\begin{array}{l}{BC=CD}\\{CE=CF}\end{array}\right.$,
∴Rt△BEC≌Rt△DFC(HL),
∴BE=DF.
(2)∵Rt△BEC≌Rt△DFC,
∴BE=DF,
∵CF⊥AF,CE⊥AB,
∴∠F=∠CEA=90°,
∵AC平分∠BAF,
∠FAC=∠EAC,
在△FAC和△EAC中
$\left\{\begin{array}{l}{∠F=∠AEC}\\{∠FAC=∠EAC}\\{AC=AC}\end{array}\right.$,
∴△FAC≌△EAC(AAS),
∴AE=AF,
设BE=x,则AE=21-x,DF=x,AF=9+x,
∴21-x=9+x,
∴x=6,即BE=6,
在Rt△BCE中,∵BC=10,BE=6,
∴由勾股定理得:CE=8.
点评 本题考查了全等三角形的性质、角平分线的性质定理等知识,解题的关键是熟练掌握全等三角形的判定方法,灵活应用所学知识解决问题,属于中考常考题型.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
12.下列说法中正确的是( )
| A. | 长方体中棱与棱不相交就是异面 | |
| B. | 长方体中相对的两个面一定是互相平行的平面 | |
| C. | “合页型折纸”通常用来检验直线与平面是否平行的 | |
| D. | 垂直于平面的直线称为铅垂线 |
6. 如图,线段AB表示一根对折以后的绳子,现从P处把绳子剪断,剪断后的各段绳子中最长的一段8cm,若AP=$\frac{1}{2}$PB,则这条绳子的原长为( )cm.
如图,线段AB表示一根对折以后的绳子,现从P处把绳子剪断,剪断后的各段绳子中最长的一段8cm,若AP=$\frac{1}{2}$PB,则这条绳子的原长为( )cm.
 如图,线段AB表示一根对折以后的绳子,现从P处把绳子剪断,剪断后的各段绳子中最长的一段8cm,若AP=$\frac{1}{2}$PB,则这条绳子的原长为( )cm.
如图,线段AB表示一根对折以后的绳子,现从P处把绳子剪断,剪断后的各段绳子中最长的一段8cm,若AP=$\frac{1}{2}$PB,则这条绳子的原长为( )cm.| A. | 12 | B. | 24 | C. | 20 或24 | D. | 12或24 |
10.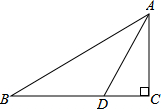 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,则BC的长为( )
如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,则BC的长为( )
 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,则BC的长为( )
如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,则BC的长为( )| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$+1 | C. | $\sqrt{5}$+1 | D. | $\sqrt{5}$-1 |
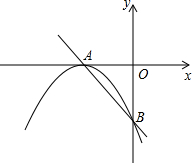 如图,直线y=-x-2交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c的顶点为A,且经过点B.
如图,直线y=-x-2交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c的顶点为A,且经过点B. 如图,在△ABC中,AD⊥BC于D,AB=4,AC=3,DC=$\frac{9}{5}$.
如图,在△ABC中,AD⊥BC于D,AB=4,AC=3,DC=$\frac{9}{5}$.