Question

5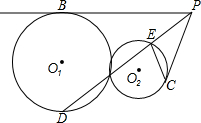．如图，⊙O₁与⊙O₂外切点A，半径为r₁，r₂，PB，PC分别为两圆的切线，B，C为切点，PB：PC=r₁：r₂，又PA交⊙O₂于点E，则下面结论不正确的是（　　）

• A． S_△PAB：S_△PCE=r₁²：r₂²
• B． PA：PD=r₂：r₁
• C． AE：AD=r₂：r₁
• D． PB：PD=r₂：r₁

Answer 1

分析 先证明△O₁PB∽△O₂PC推出△O₁AP≌△O₂EP，再由△PAB∽△PEC得$\frac{{S}_{△PAB}}{{S}_{△PCE}}$=$\frac{P{B}^{2}}{P{C}^{2}}$═$\frac{{{r}_{1}}^{2}}{{{r}_{2}}^{2}}$，故A正确；由△PO₁D∽△PO₂A得到$\frac{PA}{PD}=\frac{{O}_{2}A}{{O}_{1}D}=\frac{{r}_{2}}{{r}_{1}}$，故B正确；由△O₁AD∽△O₂AE，得$\frac{AE}{AD}$=$\frac{{O}_{2}A}{{O}_{1}A}$=$\frac{{r}_{2}}{{r}_{1}}$故C正确；由此不难判断结论．

解答 解：∵PB，PC分别为两圆的切线，
∴∠O₁BP=∠O₂CP，=90°，
∵$\frac{PB}{PC}$=$\frac{{r}_{1}}{{r}_{2}}$=$\frac{{O}_{1}B}{{O}_{2}C}$，
∴△O₁PB∽△O₂PC，
∴∠3=∠4，$\frac{P{O}_{1}}{P{O}_{2}}$=$\frac{{r}_{1}}{{r}_{2}}$=$\frac{{O}_{1}A}{{O}_{2}A}$，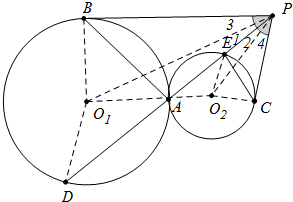
∴PA平分∠O₁PO₂，即∠1=∠2，
∴∠APB=∠APC，
∵₂OA=O₂E，
∴∠O₁AP=∠O₂EP，
∴△O₁AP≌△O₂EP，
∴$\frac{PA}{PE}$=$\frac{{r}_{1}}{{r}_{2}}$=$\frac{PB}{PC}$，
∴△PAB∽△PEC，
∴$\frac{{S}_{△PAB}}{{S}_{△PCE}}$=$\frac{P{B}^{2}}{P{C}^{2}}$═$\frac{{{r}_{1}}^{2}}{{{r}_{2}}^{2}}$；故A正确；
∵$\frac{PA}{PE}$=$\frac{{r}_{1}}{{r}_{2}}$=$\frac{{O}_{1}D}{{O}_{2}A}$，
∴△PO₁D∽△PO₂A，
∴$\frac{PA}{PD}=\frac{{O}_{2}A}{{O}_{1}D}=\frac{{r}_{2}}{{r}_{1}}$；故B正确；
∵∠O₁DA=∠O₁AD=∠O₂AE=∠O₂EA，
∴△O₁AD∽△O₂AE，
∴$\frac{AE}{AD}$=$\frac{{O}_{2}A}{{O}_{1}A}$=$\frac{{r}_{2}}{{r}_{1}}$；故C正确；
综上，不正确的选D．
故选D．

点评 本题考查了切线的性质、相似三角形的判定和性质、记住圆的切线垂直于经过切点的半径，相似三角形的面积比等于相似比的平方，解题的关键是正确寻找相似三角形，利用相似三角形的寻找解决问题，属于中考常考题型．