题目内容
1.当x=1+$\frac{1}{y}$,y=1+$\frac{1}{x}$,则y等于y1=$\frac{1+\sqrt{5}}{2}$,y2=$\frac{1-\sqrt{5}}{2}$.分析 根据x=1+$\frac{1}{y}$,y=1+$\frac{1}{x}$,两式作差,从而可以求得x与y的关系,进而可以解答本题.
解答 解:∵x=1+$\frac{1}{y}$,y=1+$\frac{1}{x}$,
∴x-y=1+$\frac{1}{y}$-1-$\frac{1}{x}$=$\frac{1}{y}-\frac{1}{x}$=$\frac{x-y}{xy}$,
∴x-y=0或xy=1,
得y=x或y=$\frac{1}{x}$,
①当y=x时,y=1+$\frac{1}{y}$,花间,得
y2-y-1=0,解得y=$\frac{1±\sqrt{5}}{2}$,
即y1=$\frac{1+\sqrt{5}}{2}$,y2=$\frac{1-\sqrt{5}}{2}$;
②当xy=1时,y=1+y方程不成立;
故答案为:y1=$\frac{1+\sqrt{5}}{2}$,y2=$\frac{1-\sqrt{5}}{2}$.
点评 本题考查分式的加减法,利用作差法得出x-y=1+$\frac{1}{y}$-1-$\frac{1}{x}$=$\frac{1}{y}-\frac{1}{x}$=$\frac{x-y}{xy}$是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.某个样本的频数分布直方图中一共有4组,从左至右的组别中,处于中间的值依次为5,8,11,14(每一组包括前一个边界值,不包括后一个边界值),频数依次为5,4,6,5.则频数为4的一组为( )
| A. | 6.5-9.5 | B. | 9.5-12.5 | C. | 8-11 | D. | 5-8 |
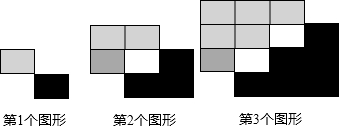
 如图,正方形是由若干个相同的长方形组成,上下各有2个水平放置的长方形,中间竖放n个长方形,则n=4.
如图,正方形是由若干个相同的长方形组成,上下各有2个水平放置的长方形,中间竖放n个长方形,则n=4. 如图是一个常见铁夹的侧面示意图,OA、OB表示铁夹的两个叶片,C是轴,CD⊥OA于点D,已知DA=40mm,DO=35mm,DC=10mm,我们知道铁夹的侧面是轴对称图形,请求出A、B两点间的距离.
如图是一个常见铁夹的侧面示意图,OA、OB表示铁夹的两个叶片,C是轴,CD⊥OA于点D,已知DA=40mm,DO=35mm,DC=10mm,我们知道铁夹的侧面是轴对称图形,请求出A、B两点间的距离.