题目内容
 如图,⊙O的半径为4,AB是弦,且∠OAB=45°,点P是
如图,⊙O的半径为4,AB是弦,且∠OAB=45°,点P是 |
| APB |
(1)求AB的长;
(2)判断∠ACB是否为定值?若是,求出∠ACB的大小;否则,请说明理由;
(3)记△ABC的面积为S,当S取得最大值时,求此时PD的长.
考点:圆的综合题
专题:综合题
分析:(1)连接OB,如图1,先证明△OAB为等腰直角三角形,然后根据等腰直角三角形的性质易得AB=4
;
(2)连接PA、PB,作圆周角∠AEB,根据圆周角定理得∠AEB=
∠AOB=45°,再根据圆内接四边形的性质得∠APB=180°-∠AEB=135°,然后根据⊙P为△ABC的内切圆,利用内心的性质得∠PAB=
∠CAB,∠PBA=
∠CBA,利用三角形的内角和定理得∠PAB+∠PBA=45°,则∠CAB+∠CBA=90°,所以∠ACB=180°-(∠CAB+∠CBA)=90°;
(3)由于AB不变,所以当C点到AB的距离最大时,S最大,此时点P为弧AB的中点,由于PD⊥AB,根据垂径定理的推理得PD经过点O,再根据等腰直角三角形的性质得OD=
AB=2
,所以PD=OP-OD=4-2
.
| 2 |
(2)连接PA、PB,作圆周角∠AEB,根据圆周角定理得∠AEB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)由于AB不变,所以当C点到AB的距离最大时,S最大,此时点P为弧AB的中点,由于PD⊥AB,根据垂径定理的推理得PD经过点O,再根据等腰直角三角形的性质得OD=
| 1 |
| 2 |
| 2 |
| 2 |
解答:解:(1)连接OB,如图,
∵OA=OB,∠OAB=45°,
∴∠OBA=45°,
∴△OAB为等腰直角三角形,
∴AB=
OA=4
;
(2)∠ACB为定值.
连接PA、PB,作圆周角∠AEB,
∵△OAB为等腰直角三角形,
∴∠AOB=90°,
∴∠AEB=
∠AOB=45°,
∴∠APB=180°-∠AEB=135°,
∵以点D为圆心、DP长为半径作⊙P,分别过点A、B作⊙P的切线,即⊙P为△ABC的内切圆,
∴PA、PB分别平分∠CAB和∠CBA,
∴∠PAB=
∠CAB,∠PBA=
∠CBA,
∵∠PAB+∠PBA=180°-∠APB=180°-135°=45°,
∴
∠CAB+
∠CBA=45°,
∴∠CAB+∠CBA=90°,
∴∠ACB=180°-(∠CAB+∠CBA)=90°;
(3)当C点到AB的距离最大时,S最大,此时点P为弧AB的中点,
∵PD⊥AB,
∴PD经过点O,
∴OD=
AB=2
,
∴PD=OP-OD=4-2
.

∵OA=OB,∠OAB=45°,
∴∠OBA=45°,
∴△OAB为等腰直角三角形,
∴AB=
| 2 |
| 2 |
(2)∠ACB为定值.
连接PA、PB,作圆周角∠AEB,
∵△OAB为等腰直角三角形,
∴∠AOB=90°,
∴∠AEB=
| 1 |
| 2 |
∴∠APB=180°-∠AEB=135°,
∵以点D为圆心、DP长为半径作⊙P,分别过点A、B作⊙P的切线,即⊙P为△ABC的内切圆,
∴PA、PB分别平分∠CAB和∠CBA,
∴∠PAB=
| 1 |
| 2 |
| 1 |
| 2 |

∵∠PAB+∠PBA=180°-∠APB=180°-135°=45°,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CAB+∠CBA=90°,
∴∠ACB=180°-(∠CAB+∠CBA)=90°;
(3)当C点到AB的距离最大时,S最大,此时点P为弧AB的中点,
∵PD⊥AB,
∴PD经过点O,
∴OD=
| 1 |
| 2 |
| 2 |
∴PD=OP-OD=4-2
| 2 |
点评:本题考查了圆的综合题:熟练掌握三角形内心的性质、垂径定理、圆周角定理和圆内接四边形的性质;会利用等腰直角三角形的性质进行计算.

练习册系列答案
相关题目
 如图,矩形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BFA=30°,那么∠AEF等于( )
如图,矩形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BFA=30°,那么∠AEF等于( )| A、60° | B、65° |
| C、70° | D、75° |

 如图,某风筝线的一端固定在地面上,此时风筝线长AB=48米,风筝线与地面的夹角∠ABC=60°,求风筝的高度AC.
如图,某风筝线的一端固定在地面上,此时风筝线长AB=48米,风筝线与地面的夹角∠ABC=60°,求风筝的高度AC.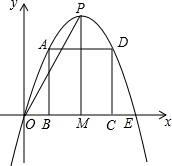 已知抛物线OPE与x轴的交点为点O、点E且OE=4,点A是抛物线OPE的一个动点(不与点O、E重合),作AB⊥X轴于点B,线段AB的最大值是PM=4.
已知抛物线OPE与x轴的交点为点O、点E且OE=4,点A是抛物线OPE的一个动点(不与点O、E重合),作AB⊥X轴于点B,线段AB的最大值是PM=4.