题目内容
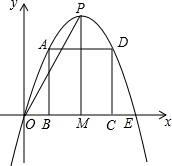 已知抛物线OPE与x轴的交点为点O、点E且OE=4,点A是抛物线OPE的一个动点(不与点O、E重合),作AB⊥X轴于点B,线段AB的最大值是PM=4.
已知抛物线OPE与x轴的交点为点O、点E且OE=4,点A是抛物线OPE的一个动点(不与点O、E重合),作AB⊥X轴于点B,线段AB的最大值是PM=4.(1)求抛物线OPE的解析式.
(2)当点A运动到什么位置时,图中的矩形ABCD是正方形?并求出点A的坐标.
(3)是否在此抛物线上存在点A使得△ABO与△PMO相似?若存在,请求出点A的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)先求出点O,E,P的坐标,利用待定系数法求解即可.
(2)设当A的坐标为(x,-x2+4x)时,矩形ABCD是正方形,利用正方形的边长相等求解.
(3)分两种情况:①当∠BAO=∠MPO时,△ABO与△PMO相似;②当∠AOB=∠MPO时,△ABO与△PMO相似;利用比例式求解.
(2)设当A的坐标为(x,-x2+4x)时,矩形ABCD是正方形,利用正方形的边长相等求解.
(3)分两种情况:①当∠BAO=∠MPO时,△ABO与△PMO相似;②当∠AOB=∠MPO时,△ABO与△PMO相似;利用比例式求解.
解答:解:∵抛物线OPE与x轴的交点为点O、点E且OE=4,
∴O(0,0),E(4,0),
∵AB⊥X轴于点B,线段AB的最大值是PM=4.
∴P(2,4),
∵抛物线OPE过原点,设它的解析式为y=ax2+bx,
把E(4,0),P(2,4),代入y=ax2+bx,得
解得
.
∴抛物线OPE的解析式为y=-x2+4x.
(2)设当A的坐标为(x,-x2+4x)时,矩形ABCD是正方形,
∵OM=2,
∴BM=2-x,
BC=2BM=2(2-x)=4-2x,
∵AB=-x2+4x,
∴-x2+4x=4-2x,解得x=3-
或x=3+
(舍去).
∴-x2+4x=2
-2,
∴点A的坐标(3-
,2
-2),
(3)存在.
设点A的坐标为(x,-x2+4x)时,△ABO与△PMO相似,
①当∠BAO=∠MPO时,
∵
=
,
∴
=
,
解得x=2或x=0(舍去),
点A的坐标为(2,4)时,即与点P重合,
②当∠AOB=∠MPO时,
∵
=
,
即
=
,解得x=
或x=0(舍去)
∴-x2+4x=
,
∴点A的坐标(
,
),
综上所述当A的坐标为(2,4)或(
,
)时,△ABO与△PMO相似.
∴O(0,0),E(4,0),
∵AB⊥X轴于点B,线段AB的最大值是PM=4.
∴P(2,4),
∵抛物线OPE过原点,设它的解析式为y=ax2+bx,
把E(4,0),P(2,4),代入y=ax2+bx,得
|
解得
|
∴抛物线OPE的解析式为y=-x2+4x.
(2)设当A的坐标为(x,-x2+4x)时,矩形ABCD是正方形,
∵OM=2,
∴BM=2-x,
BC=2BM=2(2-x)=4-2x,
∵AB=-x2+4x,
∴-x2+4x=4-2x,解得x=3-
| 5 |
| 5 |
∴-x2+4x=2
| 5 |
∴点A的坐标(3-
| 5 |
| 5 |
(3)存在.
设点A的坐标为(x,-x2+4x)时,△ABO与△PMO相似,
①当∠BAO=∠MPO时,
∵
| AB |
| PM |
| OB |
| OM |
∴
| -x2+4x |
| 4 |
| x |
| 2 |
解得x=2或x=0(舍去),
点A的坐标为(2,4)时,即与点P重合,
②当∠AOB=∠MPO时,
∵
| OB |
| PM |
| AB |
| OM |
即
| x |
| 4 |
| -x2+4x |
| 2 |
| 7 |
| 2 |
∴-x2+4x=
| 7 |
| 4 |
∴点A的坐标(
| 7 |
| 2 |
| 7 |
| 4 |
综上所述当A的坐标为(2,4)或(
| 7 |
| 2 |
| 7 |
| 4 |
点评:本题主要考查了二次函数与方程、几何知识的综合应用,涉及三角形相似,二次函数解析式及正方形性质,解题的关键是利用三角形相似列出方程.

练习册系列答案
相关题目
已知代数式x+2y的值是3,则代数式2x+4y+1的值是( )
| A、1 | B、4 | C、7 | D、不能确定 |

 如图,⊙O的半径为4,AB是弦,且∠OAB=45°,点P是
如图,⊙O的半径为4,AB是弦,且∠OAB=45°,点P是
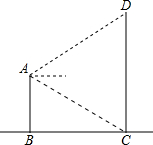 小明为了测量建筑物CD的高度,在距建筑物CD的水平距离100米的建筑物AB顶上用测角仪得从A点测得D点的仰角为26°36′,从A点测得C点的俯角为63°24′.
小明为了测量建筑物CD的高度,在距建筑物CD的水平距离100米的建筑物AB顶上用测角仪得从A点测得D点的仰角为26°36′,从A点测得C点的俯角为63°24′. 在方格纸上过C作线段CE∥AB,过D作线段DF⊥AB,且E、F在格点上.(要求用签字笔作图)
在方格纸上过C作线段CE∥AB,过D作线段DF⊥AB,且E、F在格点上.(要求用签字笔作图) 如图,已知△ABC中,∠B>∠C,AD是BC边上高,AE是∠BAC平分线,若∠
如图,已知△ABC中,∠B>∠C,AD是BC边上高,AE是∠BAC平分线,若∠