题目内容
如图所示，在△ABC中，BA=BC=20cm，AC=30cm，点P从A点出发，沿着AB以每秒4cm的速度向B点运动；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，设运动时间为x．（1）当x为何值时，PQ∥BC；
（2）当
| S△BCQ |
| S△ABC |
| 1 |
| 3 |
| S△APQ |
| S△ABC |
考点：相似三角形的判定与性质
专题：动点型
分析：（1）由PQ∥BC，得出比例式
=
，即可求出x的值；（2）由
=
，得出
=
，求出CQ=10，x=
，得出PQ∥BC，△APQ∽△ABC，即可求出
=(
)2=(
)2=
．
| AP |
| AB |
| AQ |
| AC |
| S△BCQ |
| S△ABC |
| 1 |
| 3 |
| CQ |
| AC |
| 1 |
| 3 |
| 10 |
| 3 |
| S△APQ |
| S△ABC |
| AQ |
| AB |
| 20 |
| 30 |
| 4 |
| 9 |
解答：解：（1）当PQ∥BC时，
=
，
即
=
，
解得：x=
，
因此当x=
时，PQ∥BC；
（2）当
=
时，
=
，
即
=
，∴CQ=10，
此时，x=
，AQ=AC-CQ=20，
由（1）知，PQ∥BC，
∴△APQ∽△ABC，
∴
=(
)2=(
)2=
．
| AP |
| AB |
| AQ |
| AC |
即
| 4x |
| 20 |
| 30-3x |
| 30 |
解得：x=
| 10 |
| 3 |
因此当x=
| 10 |
| 3 |
（2）当
| S△BCQ |
| S△ABC |
| 1 |
| 3 |
| CQ |
| AC |
| 1 |
| 3 |
即
| CQ |
| 30 |
| 1 |
| 3 |
此时，x=
| 10 |
| 3 |
由（1）知，PQ∥BC，
∴△APQ∽△ABC，
∴
| S△APQ |
| S△ABC |
| AQ |
| AB |
| 20 |
| 30 |
| 4 |
| 9 |
点评：本题考查了相似三角形的判定与性质；证明三角形相似得出比例式是解决问题的关键．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
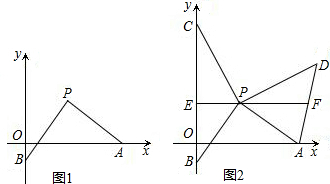
如图所示，在Rt△ABC中，∠C=90°，∠A，∠B，∠C所对的边分别是a，b，c，已知b=2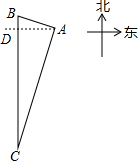
如图，某国3艘炮艇正追袭5条中国渔船，“中国渔政310”船（用“A”表示）接到陆地指挥中心（用“B”表示）命令疾速驰救中国渔船，渔船（用“C”表示）位于陆地指挥中心正南方向．经测定AB=
如图所示，圆O是Rt△ABC的外接圆，点O在AB上，BD⊥AB，点B是垂足，OD∥AC，连接CD．已知AB=5，AC=3，求DE的长．
如图，在△ABC中，D、E分别是边AB、AC上的点，DE∥BC，AD：DB=1：2，S△ADE=1，则S四边形BCED的值为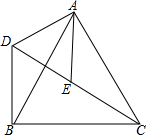
如图，△ACB和△ADE均为等边三角形，点C、E、D在同一直线上，连接BD，试猜想线段CE、BD之间的数量关系，并说明理由．
一个长方体的主视图与俯视图如图所示，则这个长方体的表面积是