题目内容
5.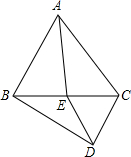 如图所示,△ABC、△DEC是等边三角形.
如图所示,△ABC、△DEC是等边三角形.(1)求证:BD=AE;
(2)若△DEC绕顶点C旋转到任何一位置时,BD与AE仍然相等吗?请说明理由.
分析 (1)根据等边三角形各边长相等性质可以证明△BDC≌△AEC,即可解题;
(2)若△DEC绕顶点C旋转到任何一位置时,BD与AE仍然相等;易证∠ACE=∠BCD,即可求证△ACE≌△BCD,即可解题.
解答 解:(1)∵△ABC、△CDE都是等边三角形.
∴∠ACE=60°,∠BCD=60°,
在△ACE和△BCD中,$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD=60°}\\{CE=CD}\end{array}\right.$,
∴△ACE≌△BCD,(SAS),
∴AE=BD;
(2)△DEC绕顶点C旋转到任何一位置时,BD与AE仍然相等,如图②,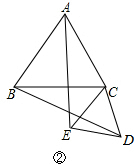
∵△ABC、△CDE都是等边三角形.
∴∠ACB=60°,∠ECD=60°,
∴∠ACE=∠BCD,
在△ACE和△BCD中,$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CE=CD}\end{array}\right.$,
∴△ACE≌△BCD,(SAS),
∴AE=BD.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACE≌△BCD是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
20.2015年9月3日,纪念中国人民抗日战争暨世界反法西斯战争胜利70周年大会在北京隆重举行.在此次活动中,共有11个徒步方队,27个装备方队12 000名官兵通过天安门广场接受党和人民的检阅.将数字12 000用科学记数法表示为( )
| A. | 12×103 | B. | 1.2×104 | C. | 1.2×105 | D. | 0.12×105 |
1.下列命题中:
①立方根等于它本身的数有-1,0,1;
②负数没有立方根;
③$\root{3}{6}$=2;
④任何正数都有两个立方根,且它们互为相反数;
⑤平方根等于它本身的数有0和1.
正确的有( )
①立方根等于它本身的数有-1,0,1;
②负数没有立方根;
③$\root{3}{6}$=2;
④任何正数都有两个立方根,且它们互为相反数;
⑤平方根等于它本身的数有0和1.
正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.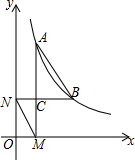 如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )
如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )
 如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )
如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )| A. | $\frac{3}{2}$ | B. | 2 | C. | 3 | D. | $\frac{9}{2}$ |
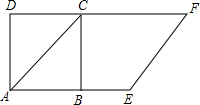 如图,以正方形ABCD的对角线AC为一边,延长AB到E,使AE=AC,以AE为一边作菱形AEFC,若菱形的面积为9$\sqrt{2}$cm2,则正方形ABCD的面积为9.
如图,以正方形ABCD的对角线AC为一边,延长AB到E,使AE=AC,以AE为一边作菱形AEFC,若菱形的面积为9$\sqrt{2}$cm2,则正方形ABCD的面积为9.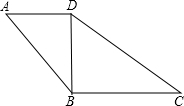 如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.
如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.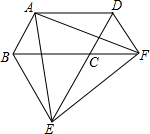 如图,在平行四边形ABCD中,△BCE、△CDF都是等边三角形,试说明△AEF是等边三角形.
如图,在平行四边形ABCD中,△BCE、△CDF都是等边三角形,试说明△AEF是等边三角形.