题目内容
 在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,连接AC、EF,证明:△ABC∽△AEF.
在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,连接AC、EF,证明:△ABC∽△AEF.考点:相似三角形的判定,平行四边形的性质
专题:证明题
分析:根据平行四边形的性质得出AB∥CD,进而得出∠B=∠EAF,根据平行四边形的性质得出∠B=∠D,再利用∠AEB=∠AFD=90°,得出△ABE∽△ADF,即可得出
=
,即可得出△ABC∽△EAF.
| AB |
| AE |
| BC |
| AF |
解答:证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAF=∠AFD=90°,
∵∠B+∠BAE=90°,∠EAF+∠BAE=90°,
∴∠B=∠EAF,
∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
∴△ABE∽△ADF,
∴
=
,
∵AD=BC,
∴
=
,
∴△ABC∽△EAF,
∴AB∥CD,
∴∠BAF=∠AFD=90°,
∵∠B+∠BAE=90°,∠EAF+∠BAE=90°,
∴∠B=∠EAF,
∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
∴△ABE∽△ADF,
∴
| AB |
| AE |
| AD |
| AF |
∵AD=BC,
∴
| AB |
| AE |
| BC |
| AF |
∴△ABC∽△EAF,
点评:此题主要考查了相似三角形的判定与性质以及平行四边形的性质等知识,根据已知得出∠B=∠EAF是解题关键.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,BO1=O1O2=O2O3=O3D.连结AO1交BC于点E,连结EO3交AD于点F,则AD:FD等于( )
如图,在平行四边形ABCD中,BO1=O1O2=O2O3=O3D.连结AO1交BC于点E,连结EO3交AD于点F,则AD:FD等于( )| A、6:1 | B、7:1 |
| C、8:1 | D、9:1 |
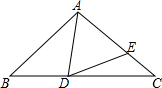 如图,已知在△ABC中,AB=AC,D是BC边上任意一点,E在AC边上,且AD=AE.
如图,已知在△ABC中,AB=AC,D是BC边上任意一点,E在AC边上,且AD=AE.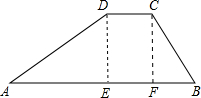 如图,一个水库大坝的横截面是梯形,其横截面的迎水坡AD的坡比为2:3,背水坡BC的坡比为4:3,大坝高DE为20m.坝顶宽CD为45m.求大坝的横截面积.
如图,一个水库大坝的横截面是梯形,其横截面的迎水坡AD的坡比为2:3,背水坡BC的坡比为4:3,大坝高DE为20m.坝顶宽CD为45m.求大坝的横截面积.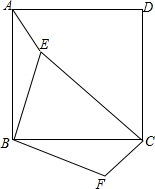 如图,已知正方形ABCD,BE=BF,∠ABE=∠CBF.
如图,已知正方形ABCD,BE=BF,∠ABE=∠CBF.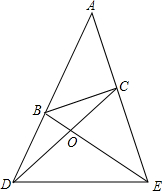 如图,已知AB:AC=AE:AD.求证:△ODB∽△OEC.
如图,已知AB:AC=AE:AD.求证:△ODB∽△OEC.