题目内容
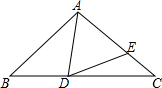 如图,已知在△ABC中,AB=AC,D是BC边上任意一点,E在AC边上,且AD=AE.
如图,已知在△ABC中,AB=AC,D是BC边上任意一点,E在AC边上,且AD=AE.(1)若∠BAD=40°,求∠EDC的度数;
(2)若∠EDC=15°,求∠BAD的度数;
(3)根据上述两小题的答案,试探索∠EDC与∠BAD的关系.
考点:等腰三角形的性质
专题:
分析:(1)根据等腰三角形性质求出∠B的度数,根据三角形的外角性质求出∠ADC,求出∠DAC,根据等腰三角形性质求出∠ADE即可;
(2)根据三角形的一个外角等于和它不相邻的两个内角的和,∠AED=∠EDC+∠C,∠ADC=∠B+∠BAD,再根据等边对等角的性质∠B=∠C,∠ADE=∠AED,代入数据计算即可求出∠BAD的度数;
(3)根据(1)(2)的结论猜出即可.
(2)根据三角形的一个外角等于和它不相邻的两个内角的和,∠AED=∠EDC+∠C,∠ADC=∠B+∠BAD,再根据等边对等角的性质∠B=∠C,∠ADE=∠AED,代入数据计算即可求出∠BAD的度数;
(3)根据(1)(2)的结论猜出即可.
解答:解:(1)∵AB=AC,
∴∠B=∠C=
(180°-∠BAC)=90°-
∠BAC,
∴∠ADC=∠B+∠BAD=90°-
∠BAC+40°=130°-
∠BAC,
∵∠DAC=∠BAC-∠BAD=∠BAC-40°,
∴∠ADE=∠AED=
(180°-∠DAC)=110°-
∠BAC,
∴∠EDC=∠ADC-∠ADE=(130°-
∠BAC)-(110°-
∠BAC)=20°,
故∠EDC的度数是20°.
(2)∠AED=∠EDC+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,
∴∠AED=∠ADE,
∵AB=AC,
∴∠B=∠C,
∴∠B+∠BAD=∠EDC+∠C+∠EDC,
即∠BAD=2∠EDC,
∵∠EDC=15°,
∴∠BAD=30°.
(3)∠EDC与∠BAD的数量关系是∠EDC=
∠BAD.
∴∠B=∠C=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ADC=∠B+∠BAD=90°-
| 1 |
| 2 |
| 1 |
| 2 |
∵∠DAC=∠BAC-∠BAD=∠BAC-40°,
∴∠ADE=∠AED=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EDC=∠ADC-∠ADE=(130°-
| 1 |
| 2 |
| 1 |
| 2 |
故∠EDC的度数是20°.
(2)∠AED=∠EDC+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,
∴∠AED=∠ADE,
∵AB=AC,
∴∠B=∠C,
∴∠B+∠BAD=∠EDC+∠C+∠EDC,
即∠BAD=2∠EDC,
∵∠EDC=15°,
∴∠BAD=30°.
(3)∠EDC与∠BAD的数量关系是∠EDC=
| 1 |
| 2 |
点评:本题主要考查学生运用等腰三角形性质,三角形的内角和定理,三角形的外角性质进行推理的能力,题目比较典型,是一道很好的题目,关键是进行推理和总结规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某地区七、八月份天气较为炎热,小华对其中连续十天每天的最高气温进行统计,依次得到以下一组数据:34,35,36,34,36,37,36,37,37,37(单位:℃),则这组数据的中位数和众数分别是( )
| A、36℃,37℃ |
| B、37℃,36℃ |
| C、36.5℃,37℃ |
| D、37℃,36.5℃ |
下列光源形成的投影不同于其他三种的是( )
| A、太阳光 | B、灯光 |
| C、探照灯光 | D、台灯 |
 如图,相距2cm的两个点A,B在直线l上,它们分别以2cm/s和1cm/s的速度在l上同时向右平移.当点A,B分别平移到点A1,B1的位置时,半径为1cm的⊙A1与半径为BB1的⊙B相切,则点A平移到点A1所用的时间为( )
如图,相距2cm的两个点A,B在直线l上,它们分别以2cm/s和1cm/s的速度在l上同时向右平移.当点A,B分别平移到点A1,B1的位置时,半径为1cm的⊙A1与半径为BB1的⊙B相切,则点A平移到点A1所用的时间为( )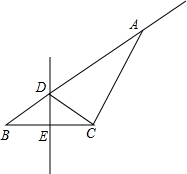 如图,在△ABC中,DE是边BC的垂直平分线,与边AB、BC交于点D、E,如果△ACD的周长为17cm,△ABC的周长为25cm,根据这些条件,你可以求出哪些线段的长?
如图,在△ABC中,DE是边BC的垂直平分线,与边AB、BC交于点D、E,如果△ACD的周长为17cm,△ABC的周长为25cm,根据这些条件,你可以求出哪些线段的长?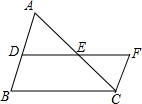 如图所示,点D是△ABC的边AB上一点,E是AC的中点,F是DE延长线上的一点,且DE=EF,连接CF,求证:∠B+∠BCF=180°.
如图所示,点D是△ABC的边AB上一点,E是AC的中点,F是DE延长线上的一点,且DE=EF,连接CF,求证:∠B+∠BCF=180°. 如图,矩形ABCD中,AE=BF=3,EF⊥ED交BC于点F,矩形的周长为22,求EF的长.
如图,矩形ABCD中,AE=BF=3,EF⊥ED交BC于点F,矩形的周长为22,求EF的长. 在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,连接AC、EF,证明:△ABC∽△AEF.
在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,连接AC、EF,证明:△ABC∽△AEF.