题目内容
19.已知△ABC的边BC=2$\sqrt{3}$cm,且△ABC内接于半径为2cm的⊙O,求∠A的度数.分析 连接OB、OC,作OD⊥BC于D,则∠ODB=90°,由垂径定理得出BD=CD=$\frac{1}{2}$BC=$\sqrt{3}$cm,由等腰三角形的性质得出∠BOD=∠COD=$\frac{1}{2}$∠BOC,由三角函数求出∠BOD=60°,得出∠BOC=120°,由圆周角定理即可得出结果.
解答 解:分两种情况: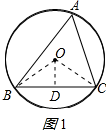
①当△ABC是锐角三角形时;连接OB、OC,作OD⊥BC于D,如图1所示:
则∠ODB=90°,BD=CD=$\frac{1}{2}$BC=$\sqrt{3}$cm,∠BOD=∠COD=$\frac{1}{2}$∠BOC,
∵sin∠BOD=$\frac{BD}{OB}=\frac{\sqrt{3}}{2}$,
∴∠BOD=60°,
∴∠BOC=120°,
∴∠A=$\frac{1}{2}$∠BOC=60°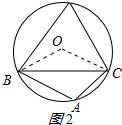
②当△ABC是钝角三角形时,如图2所示:
∠A=180°-60°=120°;
综上所述:∠A的度数为60°或120°.
点评 本题考查了三角形的外接圆、垂径定理、等腰三角形的性质、圆周角定理、三角函数等知识;本题综合性强,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
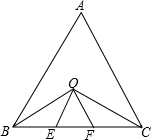 如图,等边△ABC中,OB、OC分别平分∠ABC、∠ACB,OE∥AB,OF∥AC,分别交BC于E、F.
如图,等边△ABC中,OB、OC分别平分∠ABC、∠ACB,OE∥AB,OF∥AC,分别交BC于E、F. 如图,在平面直角坐标系中,正三角形ABC的顶点坐标A(0,$\sqrt{3}$),另外两个顶点B,C在x轴上,求点B、C的坐标.
如图,在平面直角坐标系中,正三角形ABC的顶点坐标A(0,$\sqrt{3}$),另外两个顶点B,C在x轴上,求点B、C的坐标. 如图,在⊙O中,AB是直径,CD是弦,过点C作CD的垂线交AB于点E,过点D作CD的垂线交AB于点F,求证:AE=BF.
如图,在⊙O中,AB是直径,CD是弦,过点C作CD的垂线交AB于点E,过点D作CD的垂线交AB于点F,求证:AE=BF.