题目内容
10.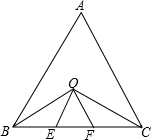 如图,等边△ABC中,OB、OC分别平分∠ABC、∠ACB,OE∥AB,OF∥AC,分别交BC于E、F.
如图,等边△ABC中,OB、OC分别平分∠ABC、∠ACB,OE∥AB,OF∥AC,分别交BC于E、F.(1)求证:△OEF是等边三角形;
(2)若AB=3,求△OEF的周长.
分析 (1)由△ABC是等边三角形,得到∠ABC=∠ACB=60°,由于OB、平分∠ABC,得到∠OBE=∠ABO=$\frac{1}{2}∠$ABC=30°,根据平行线的性质得到∠ABO=∠BOE=30°,根据三角形外角的性质得到∠OEF=∠OBE+∠BOE=60°,同理:∠OFE=60°,即可得到结论;
(2)由(1)知∠ABO=∠BOE=30°,得到OE=BE,同理OF=CF,于是得到结果.
解答 解:(1)∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵OB、平分∠ABC,
∴∠OBE=∠ABO=$\frac{1}{2}∠$ABC=30°,
∵OE∥AB,
∴∠ABO=∠BOE=30°,
∴∠OEF=∠OBE+∠BOE=60°,
同理:∠OFE=60°,
∴△OEF是等边三角形;
(2)由(1)知∠ABO=∠BOE=30°,
∴OE=BE,
同理OF=CF,
∵BC=AB=BE+EF+CF=OE+EF+OF=3,
∴△OEF的周长=3.
点评 本题考查了等边三角形的判定和性质,三角形的周长,熟练掌握等边三角形的判定和性质是解题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 如图,在等边三角形ABC中,AD为BC边上的中线,以AD为一边作等边三角形ADE,DE与AC交于点F
如图,在等边三角形ABC中,AD为BC边上的中线,以AD为一边作等边三角形ADE,DE与AC交于点F