题目内容
某旅馆有客房140间，当每间客房的日租金为60元时，每天都客满．如果一间客房的日租金增加5元，则客房每天的出租数会减少5间，当每间客房的日租金为多少元时，每日获得的总租金高达10000元？
考点：一元二次方程的应用
专题：销售问题
分析：本题中客房日租金总收入=客房日租金×租出客房数，设每间客房租金增加5x元，则每天少租客房5x÷5×5即5x间，则有每间客房日租金为（50+5x）元，租出客房数为（140-5x）间，进而可列出方程，求出答案．
解答：解：设每间客房租金增加5x元，则客房减少5x÷5×5即5x间，
依题意得方程（140-5x）（60+5x）=10000，
整理得x2-10x+25=0，
∴x1=x2=8．
租金提高5x=5×8=40．
则每日租金是60+40=100，
答：当每间客房的日租金为100元时，每日获得的总租金高达10000元．
依题意得方程（140-5x）（60+5x）=10000，
整理得x2-10x+25=0，
∴x1=x2=8．
租金提高5x=5×8=40．
则每日租金是60+40=100，
答：当每间客房的日租金为100元时，每日获得的总租金高达10000元．
点评：本题考查了一元二次方程的应用．类似商品调价问题，需把变化后客房数量及每间房的租金用含x的式子表述．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
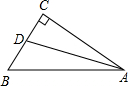已知，在Rt△ABC中，∠ACB=90°，AD平分∠BAC，AC=2
如图将图中的点（-5，2）（-4，3）（-3，4）（-2，3）（-1，2）（-2，2）（-4，2）做如下变化：