题目内容
某服装加工厂用花布加工衬衫，每块花布可裁身子25件，或袖子40只，一件身子与两只袖子可以整合成一件衬衫，现有360块花布，怎么分配花布，最多可加工多少件衬衫？
考点：二元一次方程组的应用
专题：
分析：首先根据题意设360块花布用x块裁剪身子，则（360-x）块裁剪袖子，再根据关键语句“一件身子与两只袖子可以整合成一件衬衫”可知身子数×2=袖子数，列出方程可算出用多少块花布做身子，再计算出最多可加工衬衫的件数．
解答：解：设360块花布用x块裁剪身子，则（360-x）块裁剪袖子，
25x×2=（360-x）×40，
解得：x=160，
则最多可加工衬衫的件数是：160×25=4000（件）．
答：最多可加工4000件衬衫．
25x×2=（360-x）×40，
解得：x=160，
则最多可加工衬衫的件数是：160×25=4000（件）．
答：最多可加工4000件衬衫．
点评：此题主要考查了一元一次方程的应用，关键是弄清题意，找出合适的等量关系：身子数×2=袖子数，列出方程．
练习册系列答案
相关题目
数轴上的点a，b对应的数是0，+1的相反数，点c对应的数是x，点c与点a的距离大于点c与点b的距离，则（ ）
| A、x＞0 | ||
| B、x＞-1 | ||
C、x＜-
| ||
| D、x＜-1 |
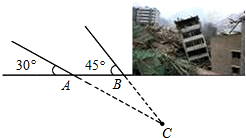某地震救援队探测出某建筑物废墟下方点C处有生命迹象，已知废墟一侧地面上两探测点A、B相距3m，探测线与地面的夹角分别是35°和45°，试确定生命所在点C的深度．（参考数据：
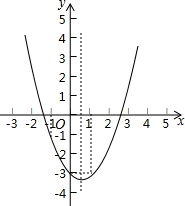已知抛物线y=ax2+bx+c的图象如图所示，