题目内容
已知直线y=-x+4,与y=
的图象交于A、B两点,O为坐标原点,求△AOB的面积.
| 3 |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:根据函数图象相交,可得方程,根据解方程,可得A、B点坐标,根据两点间距离公式,可得AB的长,根据等腰三角形的性质,可得AB边上的高,根据三角形的面积公式,可得答案.
解答:解:y=-x+4,与y=
的图象交于A、B两点,
则-x+4=
,
解得x=1或x=3,
A(1,3),B(3,1)
AB=
=2
,
△OAB是等腰三角形
O到AB的距离是2
,
S△OAB=
×2
×2
=4.
| 3 |
| x |
则-x+4=
| 3 |
| x |
解得x=1或x=3,
A(1,3),B(3,1)
AB=
| (1-3)2+(3-1)2 |
| 2 |
△OAB是等腰三角形
O到AB的距离是2
| 2 |
S△OAB=
| 1 |
| 2 |
| 2 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点问题,利用了解分式方程的方法,两点间的距离公式,三角形的面积公式.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
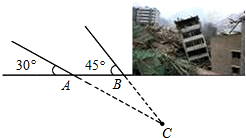 某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距3m,探测线与地面的夹角分别是35°和45°,试确定生命所在点C的深度.(参考数据:
某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距3m,探测线与地面的夹角分别是35°和45°,试确定生命所在点C的深度.(参考数据: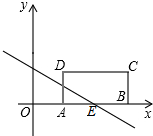 如图所示,在平面直角坐标系中,矩形ABCD的边AB位于x轴,A(1,0),B(3,0),矩形的宽AD为1,一条直线y=kx+2(k≠0)与折线ABC交于点E.
如图所示,在平面直角坐标系中,矩形ABCD的边AB位于x轴,A(1,0),B(3,0),矩形的宽AD为1,一条直线y=kx+2(k≠0)与折线ABC交于点E. 在菱形ABCD中,∠ABC=120°,对角线AC、BD交于点O,AE平分∠CAD,分别交OD、CD于F、E两点,求∠AFO的度数.
在菱形ABCD中,∠ABC=120°,对角线AC、BD交于点O,AE平分∠CAD,分别交OD、CD于F、E两点,求∠AFO的度数.