题目内容
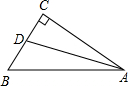 已知,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,AC=2
已知,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,AC=2| 5 |
| 4 |
| 3 |
| 15 |
考点:解直角三角形,角平分线的性质
专题:
分析:先在Rt△ABC中利用勾股定理求出CD的长,由正切函数的定义得到tan∠CAD=
=
,则∠CAD=30°,然后根据角平分线定义得出∠BAC=2∠CAD=60°,
进而求出tan∠BAC的值.
| CD |
| AC |
| ||
| 3 |
进而求出tan∠BAC的值.
解答:解:∵在Rt△ABC中,∠ACB=90°,AC=2
,AD=
,
∴CD=
=
,
∴tan∠CAD=
=
=
,
∴∠CAD=30°.
∵AD平分∠BAC,
∴∠BAC=2∠CAD=60°,
∴tan∠BAC=tan60°=
.
| 5 |
| 4 |
| 3 |
| 15 |
∴CD=
| AD2-AC2 |
2
| ||
| 3 |
∴tan∠CAD=
| CD |
| AC |
| ||||
2
|
| ||
| 3 |
∴∠CAD=30°.
∵AD平分∠BAC,
∴∠BAC=2∠CAD=60°,
∴tan∠BAC=tan60°=
| 3 |
点评:本题考查了解三角形,勾股定理,正切函数的定义,角平分线的性质,特殊角的三角函数值,难度适中.求出∠CAD=30°是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
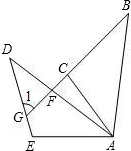 如图所示,△ABC≌△ADE,AB=AD,AC=AE,BC的延长线交DA于点F,交DE于点G,∠AED=105°,∠CAD=15°,∠B=30°,求∠1的度数.
如图所示,△ABC≌△ADE,AB=AD,AC=AE,BC的延长线交DA于点F,交DE于点G,∠AED=105°,∠CAD=15°,∠B=30°,求∠1的度数.