题目内容
20.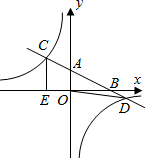 如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{2}$x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{2}$x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.(1)求反比例函数的解析式;
(2)连接OD,求△OBD的面积.
分析 (1)根据已知条件求出C点坐标,用待定系数法求出反比例的函数解析式;
(2)根据直线的解析式求得B的坐标,然后根据一次函数和反比例函数的解析式求得D的坐标,进而根据三角形的面积公式求得即可.
解答 解:(1)∵OE=2,CE⊥x轴于点E.
∴C的横坐标为-2,
把x=-2代入y=-$\frac{1}{2}$x+2得,y=-$\frac{1}{2}$×(-2)+2=3,
∴点C的坐标为C(-2,3).
设反比例函数的解析式为y=$\frac{m}{x}$,(m≠0)
将点C的坐标代入,得3=$\frac{m}{-2}$.
∴m=-6.
∴该反比例函数的解析式为y=-$\frac{6}{x}$.
(2)由直线线y=-$\frac{1}{2}$x+2可知B(4,0),
解$\left\{\begin{array}{l}{y=-\frac{1}{2}x+2}\\{y=-\frac{6}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=-2}\\{{y}_{1}=3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=6}\\{{y}_{2}=-1}\end{array}\right.$,
∴D(6,-1),
∴S△OBD=$\frac{1}{2}$×4×1=2.
点评 本题考查了待定系数法求反比例函数的解析式以及一次函数和反比例函数的交点问题,根据已知条件求得交点的坐标是解题的关键.

练习册系列答案
相关题目
10. 如图,小张与小王分别从相距300公里的甲、乙两地同时出发,相向而行.小张骑摩托车到达乙地后立即返回甲地,小王从乙地直接到达甲地.y1表示小张离甲地的距离,y2表示小王离乙地的距离.则两人从出发到第一次相遇用时( )
如图,小张与小王分别从相距300公里的甲、乙两地同时出发,相向而行.小张骑摩托车到达乙地后立即返回甲地,小王从乙地直接到达甲地.y1表示小张离甲地的距离,y2表示小王离乙地的距离.则两人从出发到第一次相遇用时( )
 如图,小张与小王分别从相距300公里的甲、乙两地同时出发,相向而行.小张骑摩托车到达乙地后立即返回甲地,小王从乙地直接到达甲地.y1表示小张离甲地的距离,y2表示小王离乙地的距离.则两人从出发到第一次相遇用时( )
如图,小张与小王分别从相距300公里的甲、乙两地同时出发,相向而行.小张骑摩托车到达乙地后立即返回甲地,小王从乙地直接到达甲地.y1表示小张离甲地的距离,y2表示小王离乙地的距离.则两人从出发到第一次相遇用时( )| A. | $\frac{24}{13}$时 | B. | $\frac{24}{11}$时 | C. | $\frac{64}{13}$时 | D. | $\frac{64}{11}$时 |
11.近两年来,绵阳房产市场呈现下滑势头,市民观望情绪严重,某楼盘开业后,发现销售形势不够理想,于是委托了专业机构对绵阳市民进行“理想房价”调查,得到如下统计图(表),请结合统计图(表)回答问题:
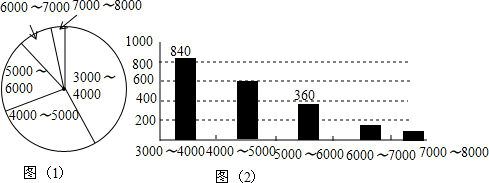
(1)该机构调查的总人数是600人,其中m=42%,认为“理想房价”在6000~7000范围内的人数n=140.在扇形统计图中,认为“理想房价”在5000~6000的扇形的圆心角是64.8°.
(2)公司销售部门分析图(表)后发现,目前楼盘开盘均价为4800元/平方米,若购房者的“实际单价”(实际单价指消费者在得到各种优惠措施后实际支出单价)为4000元/平方米时,则打破买方的心理防线,获得大多数人的认可,故提出两种促销措施,供公司领导研究采用:
①9折并送购房税(绵阳目前购房契税为总价的4%)
②降价9%并返装修款(绵阳目前装修均价约为400元/平方米)请问哪种方式能让“实际单价”降到4000元以下?
| 绵阳市理想房价调查(元/平方米) | 百分比 |
| 3000~4000 | m |
| 4000~5000 | 30% |
| 5000~6000 | 18% |
| 6000~7000 | 7% |
| 7000~8000 | 3% |

(1)该机构调查的总人数是600人,其中m=42%,认为“理想房价”在6000~7000范围内的人数n=140.在扇形统计图中,认为“理想房价”在5000~6000的扇形的圆心角是64.8°.
(2)公司销售部门分析图(表)后发现,目前楼盘开盘均价为4800元/平方米,若购房者的“实际单价”(实际单价指消费者在得到各种优惠措施后实际支出单价)为4000元/平方米时,则打破买方的心理防线,获得大多数人的认可,故提出两种促销措施,供公司领导研究采用:
①9折并送购房税(绵阳目前购房契税为总价的4%)
②降价9%并返装修款(绵阳目前装修均价约为400元/平方米)请问哪种方式能让“实际单价”降到4000元以下?
5.在二次函数y=ax2+bx+c,x与y的部分对应值如下表:
则下列说法:①图象经过原点;②图象开口向下;③图象经过点(-1,3);④当x>0时,y随x的增大而增大;⑤方程ax2+bx+c=0有两个不相等的实数根.其中正确的是( )
| x | … | -2 | 0 | 2 | 3 | … |
| y | … | 8 | 0 | 0 | 3 | … |
| A. | ①②③ | B. | ①③⑤ | C. | ①③④ | D. | ①④⑤ |
12.在Rt△ABC中,∠C=90°,若sinA=$\frac{2}{3}$,则tanB=( )
| A. | $\frac{5}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
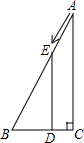 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值为4或7秒.
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值为4或7秒.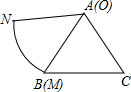 如图,扇形OMN与正三角形ABC,半径OM与AB重合,扇形弧MN的长为AB的长,已知AB=10,扇形沿着正三角形翻滚到首次与起始位置相同,则点O经过的路径长10+$\frac{70π}{3}$.
如图,扇形OMN与正三角形ABC,半径OM与AB重合,扇形弧MN的长为AB的长,已知AB=10,扇形沿着正三角形翻滚到首次与起始位置相同,则点O经过的路径长10+$\frac{70π}{3}$.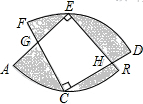 如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是弧AB的中点.若扇形的半径是2,则图中阴影部分的面积等于( )
如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是弧AB的中点.若扇形的半径是2,则图中阴影部分的面积等于( )