题目内容
5.在二次函数y=ax2+bx+c,x与y的部分对应值如下表:| x | … | -2 | 0 | 2 | 3 | … |
| y | … | 8 | 0 | 0 | 3 | … |
| A. | ①②③ | B. | ①③⑤ | C. | ①③④ | D. | ①④⑤ |
分析 结合图表可以得出当x=0或2时,y=0,x=3时,y=3,根据此三点可求出二次函数解析式,从而得出抛物线的性质.
解答 解:∵由图表可以得出当x=0或2时,y=0,x=3时,y=3,
∴$\left\{\begin{array}{l}{c=0}\\{4a+2b+c=0}\\{9a+3b+c=3}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=0}\end{array}\right.$
∴y=x2-2x,
∵c=0,∴图象经过原点,故①正确;
∵a=1>0,
∴抛物线开口向上,故②错误;
把x=-1代入得,y=3,
∴图象经过点(-1,3),故③正确;
∵抛物线的对称轴是x=1,
∴x>1时,y随x的增大而增大,x<1时,y随x的增大而减小,故④错误;
∵抛物线y=ax2+bx+c与x轴有两个交点(0,0)、(2,0)
∴ax2+bx+c=0有两个不相等的实数根,故⑤正确;
故选:B.
点评 此题主要考查了待定系数法求二次函数解析式,以及由解析式求函数与坐标轴的交点以及一元二次方程根的判别式的应用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
16.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
下列结论:其中正确的序号为(1)、(3)、(4)..
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小;
(3)3是方程ax2+(b-1)x+c=0的一个根;
(4)当-1<x<3时,ax2+(b-1)x+c>0.
| X | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小;
(3)3是方程ax2+(b-1)x+c=0的一个根;
(4)当-1<x<3时,ax2+(b-1)x+c>0.
10.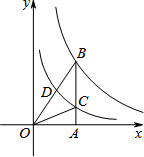 如图所示,在平面坐标系中,AB⊥x轴,反比例函数y=$\frac{{k}_{1}}{x}$(k1≠0)过B点,反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)过C、D点,OC=BC,B(2,3),则D点的坐标为( )
如图所示,在平面坐标系中,AB⊥x轴,反比例函数y=$\frac{{k}_{1}}{x}$(k1≠0)过B点,反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)过C、D点,OC=BC,B(2,3),则D点的坐标为( )
 如图所示,在平面坐标系中,AB⊥x轴,反比例函数y=$\frac{{k}_{1}}{x}$(k1≠0)过B点,反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)过C、D点,OC=BC,B(2,3),则D点的坐标为( )
如图所示,在平面坐标系中,AB⊥x轴,反比例函数y=$\frac{{k}_{1}}{x}$(k1≠0)过B点,反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)过C、D点,OC=BC,B(2,3),则D点的坐标为( )| A. | ($\frac{3}{2}$,$\frac{5}{9}$) | B. | ($\frac{\sqrt{5}}{3}$,$\frac{\sqrt{5}}{2}$) | C. | ($\frac{4}{3}$,$\frac{5}{4}$) | D. | ($\frac{\sqrt{10}}{3}$,$\frac{\sqrt{10}}{2}$) |
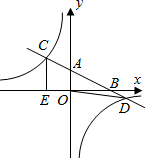 如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{2}$x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{2}$x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.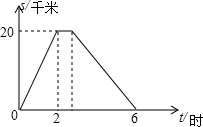 在一条笔直的公路上,依次有A、C、B三地.小明从A地途经C地前往距A地20千米的B地,到B地休息一段时间后立即按原路返回到A地.小明出发4小时的时候距离A地12千米.小明去时从C地到B地,返回时再由B地到C地(包括在B地休息的时间)共用2小时.他与A地的距离s(单位:千米)和所用的时间t(单位:小时)之间的函数关系如图所示.下列说法:①小明去时的速度为10千米/时;②小明在B地休息了$\frac{2}{3}$小时;③小明回来时的速度为6千米/时;④C地与A地的距离为15千米,其中正确的个数为( )
在一条笔直的公路上,依次有A、C、B三地.小明从A地途经C地前往距A地20千米的B地,到B地休息一段时间后立即按原路返回到A地.小明出发4小时的时候距离A地12千米.小明去时从C地到B地,返回时再由B地到C地(包括在B地休息的时间)共用2小时.他与A地的距离s(单位:千米)和所用的时间t(单位:小时)之间的函数关系如图所示.下列说法:①小明去时的速度为10千米/时;②小明在B地休息了$\frac{2}{3}$小时;③小明回来时的速度为6千米/时;④C地与A地的距离为15千米,其中正确的个数为( ) 如图,在△ABC中,∠ACB=120°,BC=2AC.
如图,在△ABC中,∠ACB=120°,BC=2AC.