题目内容
9．
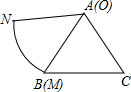如图，扇形OMN与正三角形ABC，半径OM与AB重合，扇形弧MN的长为AB的长，已知AB=10，扇形沿着正三角形翻滚到首次与起始位置相同，则点O经过的路径长10+$\frac{70π}{3}$．
分析 点O到所经过的路径分三个部分，第一部分为以点B为圆心，AB为半径，圆心角为210的弧；第二部分为10；第三部分为以点C为圆心，AC为半径，圆心角为210的弧；然后根据弧长公式进行计算．
解答 解：点O经过的路径长=$\frac{210π×10}{180}$+10+$\frac{210π×10}{180}$=10+$\frac{70}{3}$，
故答案为10+$\frac{70π}{3}$．
点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了弧长公式．
练习册系列答案
华东师大版一课一练系列答案
相关题目
如图是大型输气管的截面图（圆形），某次数学实践活动中，数学课题学习小组为了计算大型输气管的直径，在圆形弧上取了A，B两点并连接AB，在劣弧AB上取中点C连接CB，经测量$BC=\frac{5}{4}$米，∠ABC=36.87°，请根据这些数据计算出大型输气管的直径（精确到0.1米）．（sin36.87°≈0.60，cos36.87°≈0.80，tan36.87°≈0.75）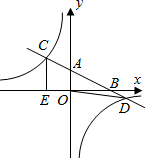
如图，在平面直角坐标系xOy中，直线y=-$\frac{1}{2}$x+2分别与x、y轴交于点B、A，与反比例函数的图象分别交于点C、D，CE⊥x轴于点E，OE=2．
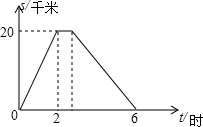在一条笔直的公路上，依次有A、C、B三地．小明从A地途经C地前往距A地20千米的B地，到B地休息一段时间后立即按原路返回到A地．小明出发4小时的时候距离A地12千米．小明去时从C地到B地，返回时再由B地到C地（包括在B地休息的时间）共用2小时．他与A地的距离s（单位：千米）和所用的时间t（单位：小时）之间的函数关系如图所示．下列说法：①小明去时的速度为10千米/时；②小明在B地休息了$\frac{2}{3}$小时；③小明回来时的速度为6千米/时；④C地与A地的距离为15千米，其中正确的个数为（ ）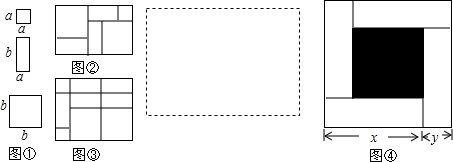
如图，在△ABC中，∠ACB=120°，BC=2AC．
如图，正方形ABCD是一块绿化带，其中阴影部分EFGH是正方形花圃．一只小鸟随机落在绿化带区域内，则它停留在花圃上的概率是$\frac{2}{9}$．