题目内容
15.某工厂开发了一种新产品,欲尽快生产9600件投入市场,该厂有甲、乙两个生产车间,甲车间每天生产的数量是乙车间的1.4倍,甲、乙两车间共同完成一半后,甲车间出现故障停产,剩下全部由乙车间单独完成结果前后共用20天完成,求甲,乙两车间每天分别能生产多少件该产品?分析 首先设乙车间每天能加工x件,则甲车间每天能加工1.4x件,由题意可得等量关系:甲乙两车间生产4800件所用的时间+乙车间生产4800件所用的时间=20天,根据等量关系可列出方程$\frac{4800}{x+1.4x}$+$\frac{4800}{x}$=20,解方程可得答案,注意不要忘记检验.
解答 解:设乙车间每天能加工x件,则甲车间每天能加工1.2x件,由题意得:
$\frac{4800}{x+1.4x}$+$\frac{4800}{x}$=20,
解得:x=340,
经检验:x=340是原分式方程的解,
1.4×340=476(件).
答:甲车间每天能加工476件,乙车间每天能加工340件.
点评 此题主要考查了分式方程的应用,关键是正确理解题意,找出题目中的等量关系,再列出方程.列分式方程解应用题的一般步骤:设、列、解、验、答,必须严格按照这5步进行做题,规范解题步骤,另外还要注意完整性.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
3.等腰三角形的一边等于3,一边等于6,则它的周长为( )
| A. | 12 | B. | 12或15 | C. | 15或18 | D. | 15 |
10.将抛物线y=x2向右平移3个单位得到的抛物线表达式是( )
| A. | y=(x-3)2 | B. | y=(x+3)2 | C. | y=x2-3 | D. | y=x2+3 |
5.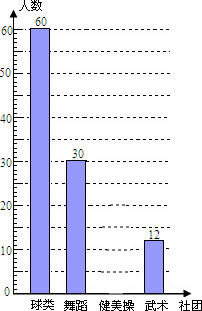 为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
(1)求样本容量及表格中m、n的值;
(2)请补全统计图;
(3)被调查的60个喜欢球类同学中有3人最喜欢足球,若该校有3200名学生,请估计该校最喜欢足球的人数.
 为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:| 社团类别 | 人数 | 占总人数比例 |
| 球类 | 60 | m |
| 舞蹈 | 30 | 0.25 |
| 健美操 | n | 0.15 |
| 武术 | 12 | 0.1 |
(2)请补全统计图;
(3)被调查的60个喜欢球类同学中有3人最喜欢足球,若该校有3200名学生,请估计该校最喜欢足球的人数.
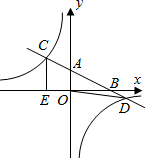 如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{2}$x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{2}$x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.