题目内容
10.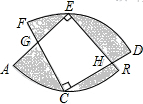 如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是弧AB的中点.若扇形的半径是2,则图中阴影部分的面积等于( )
如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是弧AB的中点.若扇形的半径是2,则图中阴影部分的面积等于( )| A. | 2π-4 | B. | 2π-2 | C. | π+4 | D. | π-1 |
分析 根据扇形的面积公式求出面积,再过点C作CM⊥AE,作CN⊥BE,垂足分别为M、N,然后证明△CMG与△CNH全等,从而得到中间空白区域的面积等于以2为对角线的正方形的面积,从而得出阴影部分的面积.
解答 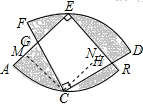 解:两扇形的面积和为:$\frac{80π×{2}^{2}}{360}$=2π,
解:两扇形的面积和为:$\frac{80π×{2}^{2}}{360}$=2π,
过点C作CM⊥AE,作CN⊥BE,垂足分别为M、N,
则四边形EMCN是矩形,
∵点C是$\widehat{AB}$的中点,
∴EC平分∠AEB,
∴CM=CN,
∴矩形EMCN是正方形,
∵∠MCG+∠FCN=90°,∠NCH+∠FCN=90°,
∴∠MCG=∠NCB,
在△CMG与△CNH中,
$\left\{\begin{array}{l}{∠MCG=∠NCH}\\{CM=CN}\\{∠CMG=∠CNB=90°}\end{array}\right.$,
∴△CMG≌△CNH(ASA),
∴中间空白区域面积相当于对角线是2的正方形面积,
∴空白区域的面积为:$\frac{1}{2}$×2×2=2,
∴图中阴影部分的面积=两个扇形面积和-2个空白区域面积的和=2π-4.
故选:A.
点评 此题主要考查了扇形的面积求法以及三角形的面积等知识,得出四边形EGCH的面积是解决问题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
5.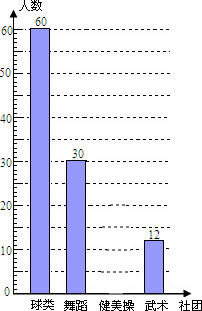 为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
(1)求样本容量及表格中m、n的值;
(2)请补全统计图;
(3)被调查的60个喜欢球类同学中有3人最喜欢足球,若该校有3200名学生,请估计该校最喜欢足球的人数.
 为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:| 社团类别 | 人数 | 占总人数比例 |
| 球类 | 60 | m |
| 舞蹈 | 30 | 0.25 |
| 健美操 | n | 0.15 |
| 武术 | 12 | 0.1 |
(2)请补全统计图;
(3)被调查的60个喜欢球类同学中有3人最喜欢足球,若该校有3200名学生,请估计该校最喜欢足球的人数.
20.若二元一次方程式组$\left\{\begin{array}{l}{5x-y=5}\\{y=\frac{1}{5}x}\end{array}\right.$的解为x=a,y=b,则a+b等于( )
| A. | $\frac{5}{4}$ | B. | $\frac{75}{13}$ | C. | $\frac{31}{25}$ | D. | $\frac{29}{25}$ |
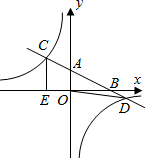 如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{2}$x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{2}$x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2. 如图,正方形ABCD是一块绿化带,其中阴影部分EFGH是正方形花圃.一只小鸟随机落在绿化带区域内,则它停留在花圃上的概率是$\frac{2}{9}$.
如图,正方形ABCD是一块绿化带,其中阴影部分EFGH是正方形花圃.一只小鸟随机落在绿化带区域内,则它停留在花圃上的概率是$\frac{2}{9}$.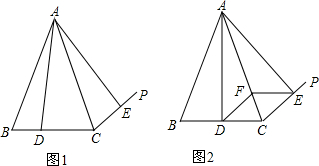
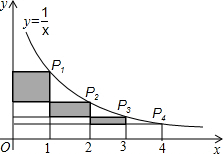 在反比例函数y=$\frac{1}{x}$(x>0)的图象上,有点P1,P2,…,P2011,…,它们的横坐标依次为1,2,…2011,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,…,S2010…,则S1+S2+…+S2010=$\frac{2010}{2011}$.
在反比例函数y=$\frac{1}{x}$(x>0)的图象上,有点P1,P2,…,P2011,…,它们的横坐标依次为1,2,…2011,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,…,S2010…,则S1+S2+…+S2010=$\frac{2010}{2011}$.