题目内容
7.先化简($\frac{{x}^{2}-2x+1}{{x}^{2}-1}$+$\frac{1}{x}$)÷$\frac{1}{x+1}$,再把x=$\sqrt{2}$代入求原式的值.分析 根据分式的混合运算法则、通分和约分法则把原式化简,代入已知数据计算即可.
解答 解:原式=$\frac{({x-1)}^{2}}{(x+1)(x-1)}$×(x+1)+$\frac{1}{x}$×(x+1)
=x-1+$\frac{x+1}{x}$,
=$\frac{{x}^{2}-x}{x}$+$\frac{x+1}{x}$
=$\frac{{x}^{2}+1}{x}$,
当x=$\sqrt{2}$时,原式=$\frac{2+1}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,掌握分式的混合运算法则、通分和约分法则以及二次根式的运算法则是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.制动距离是汽车处于某一时速的情况下,从开始刹车制动到汽车完全静止时,车辆所开过的路程,对某辆汽车进行测试时,汽车的行驶速度与汽车的制动距离的数据如表所示
(1)该汽车的制动距离s是变量还是常量?
(2)若s是v的一次函数,求s关于v的函数解析式.
| 汽车行驶速度v(千米/小时) | 30 | 40 | 50 | 60 | 70 |
| 制动距离s(米) | 5 | 12 | 19 | 26 | 33 |
(2)若s是v的一次函数,求s关于v的函数解析式.
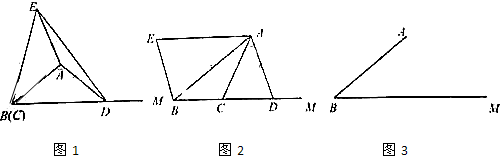
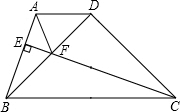 如图,在梯形ABCD中,AD∥BC,CE⊥AB于E,△BDC为等腰直角三角形,∠BDC=90°,BD=CD,CE与BD交于F,连接AF,求证:CF=AB+AF.
如图,在梯形ABCD中,AD∥BC,CE⊥AB于E,△BDC为等腰直角三角形,∠BDC=90°,BD=CD,CE与BD交于F,连接AF,求证:CF=AB+AF.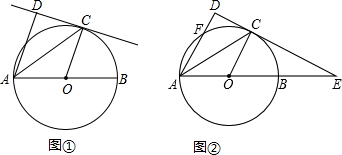
 已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C地,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发xh后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.
已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C地,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发xh后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.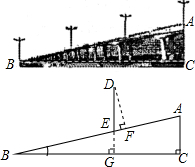 如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°.
如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°.