题目内容
19.已知A,B,C是⊙O上的三个点,CD切⊙O于点C,AC平分∠DAB.(Ⅰ)如图①,求∠ADC的大小;
(Ⅱ)如图②,延长DC,与AB的延长线交与点E,AD交⊙O于点F,若AD=4,AE=12,求⊙O的半径及AF的长.
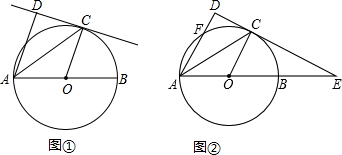
分析 (1)如图①,先证明OC∥AD,再根据切线的性质得到OC⊥CD,则AD⊥CD,然后根据垂直的定义得到∠ADC的度数;
(2)连接BF,如图②,设⊙O的半径为r,则OE=AE-OA=12-r,先证明△EOC∽△EAD,利用相似比可计算出r=3,然后证明△ABF∽△AED,利用相似比可计算出AF.
解答 解:(1) 如图①,
如图①,
∵AC平分∠DAB,
∴∠2=∠3,
∵OA=OC,
∴∠1=∠2,
∴∠1=∠3,
∴OC∥AD,
∵CD切⊙O于点C,
∴OC⊥CD,
∴AD⊥CD,
∴∠ADC=90°;
(2)连接BF,如图②,设⊙O的半径为r,则OE=AE-OA=12-r,
∵OC∥AD,
∴△EOC∽△EAD,
∴$\frac{OC}{AD}$=$\frac{OE}{AE}$,即$\frac{r}{4}$=$\frac{12-r}{12}$,解得r=3,
∵AB为直径,
∴∠AFB=90°,
∴BF∥DE,
∴△ABF∽△AED,
∴$\frac{AF}{AD}$=$\frac{AB}{AE}$,即$\frac{AF}{4}$=$\frac{6}{12}$,解得AF=2,
即⊙O的半径及AF的长分别为3和2.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.解决(2)小题的关键是灵活运用相似比计算线段的长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
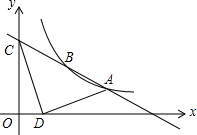 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于A(4,1)、B(2,2)两点,一次函数的图象与y轴的交点为C.
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于A(4,1)、B(2,2)两点,一次函数的图象与y轴的交点为C.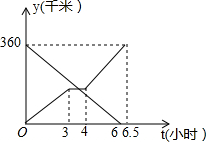 一辆货车从甲地向乙地行驶,一辆小轿车与该货车同时出发,从乙地向甲地行驶,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至甲地,货车与乙地的距离y1(千米)、小轿车与乙地的距离y2(千米)与行驶时间((小时)之间的函数关系的图象如图所示,已知当小轿车行驶2小时时,小轿车与货车相距140千米.
一辆货车从甲地向乙地行驶,一辆小轿车与该货车同时出发,从乙地向甲地行驶,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至甲地,货车与乙地的距离y1(千米)、小轿车与乙地的距离y2(千米)与行驶时间((小时)之间的函数关系的图象如图所示,已知当小轿车行驶2小时时,小轿车与货车相距140千米.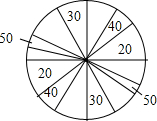 某商场搞促销活动,规定凡购物满200元就有一次摇奖机会,摇奖的转盘如图所示.转盘上写有礼券金额,其中20元、30元、40元、50元礼券所对应的扇形的圆心角之和依次为80°、60°、40°、20°.计算:
某商场搞促销活动,规定凡购物满200元就有一次摇奖机会,摇奖的转盘如图所示.转盘上写有礼券金额,其中20元、30元、40元、50元礼券所对应的扇形的圆心角之和依次为80°、60°、40°、20°.计算: