题目内容
15.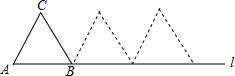 边长为1的等边△ABC在直线l上,按如图所示的方式进行两次旋转,在两次旋转过程中,点C经过的路径长为( )
边长为1的等边△ABC在直线l上,按如图所示的方式进行两次旋转,在两次旋转过程中,点C经过的路径长为( )| A. | $\frac{1}{3}$π | B. | $\frac{2}{3}$π | C. | π | D. | $\frac{4}{3}$π |
分析 根据△ABC是等比三角形可知∠CBF=120°,故第一次点C旋转的角度是120°,第二次是以点C为旋转中心,故点C未动,再由弧长公式即可得出结论.
解答 解:∵△ABC是等比三角形,
∴∠CBF=120°,
∴点C经过的路径长=$\frac{120π}{180}$=$\frac{2}{3}$π.
故选B.
点评 本题考查的是弧长的计算,熟记弧长公式是解答此题的关键.

练习册系列答案
相关题目
10.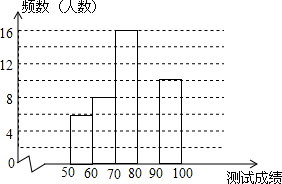 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写100个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写100个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
(1)求表中a的值;请把频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.
 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写100个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写100个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 4 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 16 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
(1)求表中a的值;请把频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.
20.下列计算正确的是( )
| A. | 2$\sqrt{\frac{1}{2}}$=$\sqrt{2}$ | B. | $\sqrt{2}$$+\sqrt{3}$=$\sqrt{5}$ | C. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | D. | 3+2$\sqrt{2}$=5$\sqrt{2}$ |
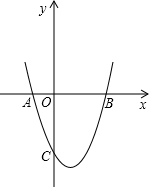 如图,二次函数y=x2+bx+c与坐标轴交于点A、B、C,且OB=OC=3.
如图,二次函数y=x2+bx+c与坐标轴交于点A、B、C,且OB=OC=3.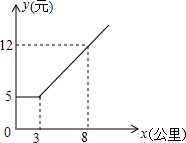 某市出租车公司收费标准如图所示,x(公里)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:
某市出租车公司收费标准如图所示,x(公里)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题: