题目内容
7.半径为2的等边三角形的边长为2$\sqrt{3}$,中心角是120°,面积是3$\sqrt{3}$.分析 连接OB,作OD⊥BC于D,则∠ODB=90°,由等边三角形的性质得出∠OBD=30°,BD=$\frac{1}{2}$BC,由三角函数求出OD的数值,再由含30°角的直角三角形的性质得出OB=2OD,即可得出结果.
解答 解:连接OB,作OD⊥BC于D,如图所示: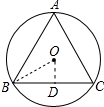
则∠ODB=90°,∠OBD=$\frac{1}{2}$∠ABC=30°,BD=CD=$\frac{1}{2}$BC,
∵OB=2,
∴OD=1,
∴BD=$\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$,
BC=2$\sqrt{3}$,
面积=$\frac{1}{2}×2\sqrt{3}×3=3\sqrt{3}$,
中心角是120°,
故答案为:2$\sqrt{3}$;120;3$\sqrt{3}$
点评 本题考查了等边三角形与圆、等边三角形的性质、三角函数、含30°角的直角三角形的性质;熟练掌握等边三角形的性质,由三角函数求出OD是解决问题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
18.某中学初一男生测试引体向上,以10个为标准,超过的个数用正数表示,不足的个数用负数表示,其中6名男生的成绩如下:(单位:个)
(1)这6名男生有几名达到标准,达标率为百分之几?
(2)他们共做了多少个引体向上?
| +3 | -4 | 0 | -2 | +4 | -1 |
(2)他们共做了多少个引体向上?
15.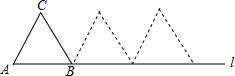 边长为1的等边△ABC在直线l上,按如图所示的方式进行两次旋转,在两次旋转过程中,点C经过的路径长为( )
边长为1的等边△ABC在直线l上,按如图所示的方式进行两次旋转,在两次旋转过程中,点C经过的路径长为( )
 边长为1的等边△ABC在直线l上,按如图所示的方式进行两次旋转,在两次旋转过程中,点C经过的路径长为( )
边长为1的等边△ABC在直线l上,按如图所示的方式进行两次旋转,在两次旋转过程中,点C经过的路径长为( )| A. | $\frac{1}{3}$π | B. | $\frac{2}{3}$π | C. | π | D. | $\frac{4}{3}$π |
12.在下列各组图形中,一定全等的是( )
| A. | 所有的直角三角形 | |
| B. | 两个等边三角形 | |
| C. | 各有一条边相等,且有一个角为100°的两个等腰三角形 | |
| D. | 斜边和一锐角对应相等的两个直角三角形 |
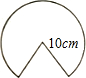 如图,从半径为10cm的圆形纸片上剪去$\frac{1}{5}$圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为6cm.
如图,从半径为10cm的圆形纸片上剪去$\frac{1}{5}$圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为6cm.