题目内容
6.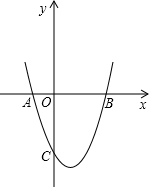 如图,二次函数y=x2+bx+c与坐标轴交于点A、B、C,且OB=OC=3.
如图,二次函数y=x2+bx+c与坐标轴交于点A、B、C,且OB=OC=3.(1)求此二次函数的解析式.
(2)写出顶点坐标和对称轴.
(3)点M、N在y=ax2+bx+c的图象上(点N在点M的右边),且MN∥x轴,求以MN为直径且与x轴相切的圆的半径.
分析 (1)由OB=OC=3,可知两点的坐标分别为B(3,0),C(0,-3),用待定系数法求得解析式;
(2)把解析式变换成顶点式,写出坐标;
(3)由(2)知,对称轴为x=1,当MN在x轴下方时,设圆半径为r,则点N的坐标为(1+r,-r),代入解析式求得r的值,同理求得当MN在x轴上方时r的值.
解答 解:(1)∵OB=OC=3,
∴B(3,0),C(0,-3),
把B(3,0),C(0,-3)分别代入y=x2+bx+c,得$\left\{\begin{array}{l}{9+3b+c=0}\\{c=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$.
故此二次函数的解析式为y=x2-2x-3;
(2)y=x2-2x-3=(x-1)2-4, 故顶点坐标(1,-4),对称轴x=1;
故顶点坐标(1,-4),对称轴x=1;
(3)设圆半径为r,
当MN在x轴下方时,N点坐标为(1+r,-r),
把N点代入y=x2-2x-3得r=$\frac{-1+\sqrt{17}}{2}$,
当MN在x轴上方时,N点坐标为(1+r,r),
把N点代入y=x2-2x-3得r=$\frac{1+\sqrt{17}}{2}$.
故圆的半径为$\frac{-1+\sqrt{17}}{2}$或$\frac{1+\sqrt{17}}{2}$.
点评 考查了二次函数综合题,解题关键是利用了待定系数法求函数的解析式,二次函数的图象与圆的关系,相切的概念求解.

练习册系列答案
相关题目
1.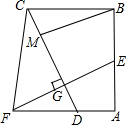 已知直角梯形ABCF中,AF∥BC,∠ABC=90°,点E为AB的中点,CD垂直平分EF于G,交AF于D,M为CG上一点,MG=EG,连BM下列结论:①若AE=AF,则CD=EF;②若EF=$\sqrt{2}$BM,则AB=AF;③若AE=2$\sqrt{2}$AD,则BC=5AD.其中正确的是( )
已知直角梯形ABCF中,AF∥BC,∠ABC=90°,点E为AB的中点,CD垂直平分EF于G,交AF于D,M为CG上一点,MG=EG,连BM下列结论:①若AE=AF,则CD=EF;②若EF=$\sqrt{2}$BM,则AB=AF;③若AE=2$\sqrt{2}$AD,则BC=5AD.其中正确的是( )
 已知直角梯形ABCF中,AF∥BC,∠ABC=90°,点E为AB的中点,CD垂直平分EF于G,交AF于D,M为CG上一点,MG=EG,连BM下列结论:①若AE=AF,则CD=EF;②若EF=$\sqrt{2}$BM,则AB=AF;③若AE=2$\sqrt{2}$AD,则BC=5AD.其中正确的是( )
已知直角梯形ABCF中,AF∥BC,∠ABC=90°,点E为AB的中点,CD垂直平分EF于G,交AF于D,M为CG上一点,MG=EG,连BM下列结论:①若AE=AF,则CD=EF;②若EF=$\sqrt{2}$BM,则AB=AF;③若AE=2$\sqrt{2}$AD,则BC=5AD.其中正确的是( )| A. | 只有①② | B. | 只有②③ | C. | 只有①③ | D. | ①②③ |
18.某中学初一男生测试引体向上,以10个为标准,超过的个数用正数表示,不足的个数用负数表示,其中6名男生的成绩如下:(单位:个)
(1)这6名男生有几名达到标准,达标率为百分之几?
(2)他们共做了多少个引体向上?
| +3 | -4 | 0 | -2 | +4 | -1 |
(2)他们共做了多少个引体向上?
15.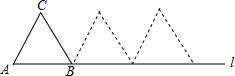 边长为1的等边△ABC在直线l上,按如图所示的方式进行两次旋转,在两次旋转过程中,点C经过的路径长为( )
边长为1的等边△ABC在直线l上,按如图所示的方式进行两次旋转,在两次旋转过程中,点C经过的路径长为( )
 边长为1的等边△ABC在直线l上,按如图所示的方式进行两次旋转,在两次旋转过程中,点C经过的路径长为( )
边长为1的等边△ABC在直线l上,按如图所示的方式进行两次旋转,在两次旋转过程中,点C经过的路径长为( )| A. | $\frac{1}{3}$π | B. | $\frac{2}{3}$π | C. | π | D. | $\frac{4}{3}$π |