题目内容
20.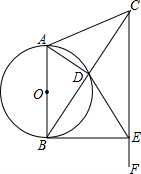 如图,在等腰△ABC中,AB=AC,以AB为直径的圆O交BC于点D,过点C作CF∥AB,与⊙O的切线BE交于点E,连接DE.
如图,在等腰△ABC中,AB=AC,以AB为直径的圆O交BC于点D,过点C作CF∥AB,与⊙O的切线BE交于点E,连接DE.(1)求证:BD=CD;
(2)求证:△CAB∽△CDE;
(3)设△ABC的面积为S1,△CDE的面积为S2,直径AB的长为x,若∠ABC=30°,S1、S2 满足S1+S2=$28\sqrt{3}$,试求x的值.
分析 (1)因为AB=AC,欲证明BD=DC,只要证明AD⊥BC即可.
(2)可以根据两角对应相等的两个三角形相似进行证明.
(3)分别用x表示S1、S2,列出方程即可解决问题.
解答 (1)证明:∵AB是直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD.
(2)∵AB∥CE,
∴∠2=∠1,
∵AB=AC,
∴∠1=∠3,
∵BE是⊙O切线,
∴∠ABE=90°,
∵AB∥CE,
∴∠BEC+∠ABE=90°,
∴∠BEC=90°,
∵BD=DC,
∴DE=DB=DC,
∴∠2=∠4,
∴∠3=∠2,∠1=∠4,
∴△CAB∽△CDE.
(3)∵S1=$\frac{1}{2}$$•\sqrt{3}$x•$\frac{1}{2}$x=$\frac{\sqrt{3}}{4}$x2.
∵△CAB∽△CDE,
∴$\frac{{S}_{1}}{{S}_{2}}$=($\frac{x}{\frac{\sqrt{3}}{2}x}$)2=$\frac{4}{3}$,
∴S2=$\frac{3\sqrt{3}}{16}$x2,
由题意:$\frac{\sqrt{3}}{4}$x2+$\frac{3\sqrt{3}}{16}$x2=28$\sqrt{3}$,
∴x=±8,
∵x>0,
∴x=8.
点评 本题考查圆的综合题、等腰三角形的判定和性质、相似三角形的判定和性质、平行线的性质等知识,解题的关键是灵活运用这些知识解决问题,属于基础题目,难度不大,是中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.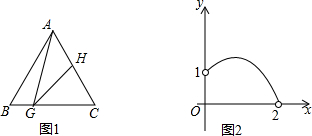 如图1,在等边三角形ABC中,AB=2,G是BC边上一个动点且不与点B、C重合,H是AC边上一点,且∠AGH=30°.设BG=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图2所示,则这条线段可能是图中的( )
如图1,在等边三角形ABC中,AB=2,G是BC边上一个动点且不与点B、C重合,H是AC边上一点,且∠AGH=30°.设BG=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图2所示,则这条线段可能是图中的( )
 如图1,在等边三角形ABC中,AB=2,G是BC边上一个动点且不与点B、C重合,H是AC边上一点,且∠AGH=30°.设BG=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图2所示,则这条线段可能是图中的( )
如图1,在等边三角形ABC中,AB=2,G是BC边上一个动点且不与点B、C重合,H是AC边上一点,且∠AGH=30°.设BG=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图2所示,则这条线段可能是图中的( )| A. | 线段CG | B. | 线段AG | C. | 线段AH | D. | 线段CH |
5.有下列四个命题:
①相等的角是对顶角;
②两条直线被第三条直线所截,同位角相等;
③过一点有且只有一条直线与已知直线平行;
④在同一平面内,垂直于同一条直线的两条直线互相平行.
其中真命题的个数为( )
①相等的角是对顶角;
②两条直线被第三条直线所截,同位角相等;
③过一点有且只有一条直线与已知直线平行;
④在同一平面内,垂直于同一条直线的两条直线互相平行.
其中真命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.若x=2是关于一元二次方程-x2+$\frac{3}{2}ax$+a2=0的一个根,则a的值是( )
| A. | 1或4 | B. | 1或-4 | C. | -1或-4 | D. | -1或4 |
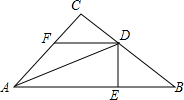 如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E,BD=DF.求证:BE=CF.
如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E,BD=DF.求证:BE=CF.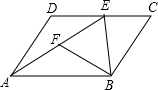 如图,在?ABCD中,过点B作BE⊥DC于点E,连接AE,F为AE上一点,且∠BFE=∠C.
如图,在?ABCD中,过点B作BE⊥DC于点E,连接AE,F为AE上一点,且∠BFE=∠C.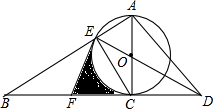 如图,已知以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
如图,已知以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.