题目内容
10.若x=2是关于一元二次方程-x2+$\frac{3}{2}ax$+a2=0的一个根,则a的值是( )| A. | 1或4 | B. | 1或-4 | C. | -1或-4 | D. | -1或4 |
分析 把x=2代入已知方程,列出关于a的新方程,通过解新方程可以求得a的值.
解答 解:∵x=2是关于x的一元二次方程-x2+$\frac{3}{2}ax$+a2=0的一个根,
∴-22+$\frac{3}{2}$a×2+a2=0,即a2+3a-4=0,
整理,得(a-1)(a+4)=0,
解得 a1=1,a2=-4.
即a的值是1或-4.
故选:B.
点评 本题考查了一元二次方程的解的定义.能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.

练习册系列答案
相关题目
1.在下列各式中,3$\sqrt{2}$的同类二次根式是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $\sqrt{20}$ |
5.若正比例函数y=kx与y=2x的图象关于x轴对称,则k的值等于( )
| A. | $\frac{1}{2}$ | B. | -2 | C. | -$\frac{1}{2}$ | D. | 2 |
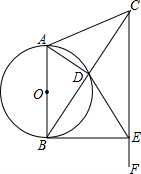 如图,在等腰△ABC中,AB=AC,以AB为直径的圆O交BC于点D,过点C作CF∥AB,与⊙O的切线BE交于点E,连接DE.
如图,在等腰△ABC中,AB=AC,以AB为直径的圆O交BC于点D,过点C作CF∥AB,与⊙O的切线BE交于点E,连接DE.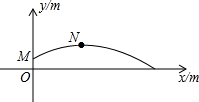 2015年10月22日,第一届全国青年运动会田径项目展开首金争夺,在男子铅球项目上,孙帅以20.39米的成绩力压群雄,摘得青年运动会田径项目首枚金牌.孙帅在赛后的一次投掷铅球的训练时,铅球经过的抛物线如图所示,其中出手点M的坐标为(0,$\frac{9}{5}$),铅球在最高点N的坐标为(9,$\frac{144}{35}$).(提示:$\sqrt{576}$=24)
2015年10月22日,第一届全国青年运动会田径项目展开首金争夺,在男子铅球项目上,孙帅以20.39米的成绩力压群雄,摘得青年运动会田径项目首枚金牌.孙帅在赛后的一次投掷铅球的训练时,铅球经过的抛物线如图所示,其中出手点M的坐标为(0,$\frac{9}{5}$),铅球在最高点N的坐标为(9,$\frac{144}{35}$).(提示:$\sqrt{576}$=24) 四张质地相同的卡片上如图所示,将卡片洗匀后,背面朝上放置在桌面上.
四张质地相同的卡片上如图所示,将卡片洗匀后,背面朝上放置在桌面上.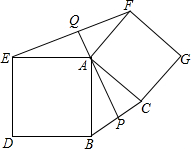 如图,两个正方形ABDE和ACGF,点P为BC中点,连接PA交EF于点Q,试探究AP与EF的数量和位置关系,并证明你的结论.
如图,两个正方形ABDE和ACGF,点P为BC中点,连接PA交EF于点Q,试探究AP与EF的数量和位置关系,并证明你的结论.