题目内容
5.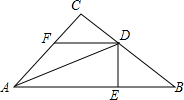 如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E,BD=DF.求证:BE=CF.
如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E,BD=DF.求证:BE=CF.
分析 根据角平分线的性质得出DE=CD,再根据HL证明Rt△BDE≌Rt△FDC,即可得出结论.
解答 证明:∵∠ACB=90°,
∴DC⊥AC,
∵AD平分∠BAC,DE⊥AB于E,
∴DE=DC.
在Rt△BDE和Rt△FDC中,
$\left\{\begin{array}{l}{BD=DF}\\{DE=DC}\end{array}\right.$,
∴Rt△BDE≌Rt△FDC(HL),
∴BE=CF.
点评 本题主要考查角平分线的性质,全等三角形的判定与性质.证明三角形全等是解答本题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
15.若tan40°=a,则tan50°=( )
| A. | $\frac{1}{a}$ | B. | -a | C. | a | D. | 2a |
17.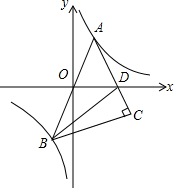 如图,点A在反比例函数y=$\frac{6}{x}$图象第一象限的分支上,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,若△OAD与△BCD的面积相等,则点A的横坐标是( )
如图,点A在反比例函数y=$\frac{6}{x}$图象第一象限的分支上,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,若△OAD与△BCD的面积相等,则点A的横坐标是( )
 如图,点A在反比例函数y=$\frac{6}{x}$图象第一象限的分支上,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,若△OAD与△BCD的面积相等,则点A的横坐标是( )
如图,点A在反比例函数y=$\frac{6}{x}$图象第一象限的分支上,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,若△OAD与△BCD的面积相等,则点A的横坐标是( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{6}$ | D. | 2$\sqrt{3}$ |
14.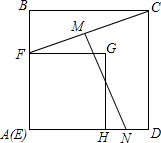 如图,面积为9cm2的正方形EFGH在面积为25cm2的正方形ABCD所在平面上移动,始终保持EF∥AB,记线段CF的中点为M,DH的中点为N,则线段MN的长度是( )
如图,面积为9cm2的正方形EFGH在面积为25cm2的正方形ABCD所在平面上移动,始终保持EF∥AB,记线段CF的中点为M,DH的中点为N,则线段MN的长度是( )
 如图,面积为9cm2的正方形EFGH在面积为25cm2的正方形ABCD所在平面上移动,始终保持EF∥AB,记线段CF的中点为M,DH的中点为N,则线段MN的长度是( )
如图,面积为9cm2的正方形EFGH在面积为25cm2的正方形ABCD所在平面上移动,始终保持EF∥AB,记线段CF的中点为M,DH的中点为N,则线段MN的长度是( )| A. | $\frac{25}{4}$cm | B. | $\frac{73}{4}$cm | C. | $\frac{\sqrt{73}}{2}$cm | D. | $\frac{\sqrt{75}}{2}$cm |
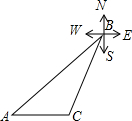 如图,某海洋区域内有A、B两个小岛,其中A岛在B岛的西南方向,一天,一只轮船上午8时从A岛出发,沿正东方向以每小时80海里的速度航行1.5小时到达C处,此时轮船在B岛的南偏西15°方向,试求A、B两岛相距多少海里?(结果保留根号)(注:E-东方,W-西方,S-南方,N-北方)
如图,某海洋区域内有A、B两个小岛,其中A岛在B岛的西南方向,一天,一只轮船上午8时从A岛出发,沿正东方向以每小时80海里的速度航行1.5小时到达C处,此时轮船在B岛的南偏西15°方向,试求A、B两岛相距多少海里?(结果保留根号)(注:E-东方,W-西方,S-南方,N-北方)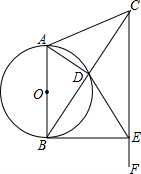 如图,在等腰△ABC中,AB=AC,以AB为直径的圆O交BC于点D,过点C作CF∥AB,与⊙O的切线BE交于点E,连接DE.
如图,在等腰△ABC中,AB=AC,以AB为直径的圆O交BC于点D,过点C作CF∥AB,与⊙O的切线BE交于点E,连接DE.