题目内容
14.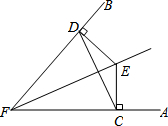 已知:E是∠AFB的平分线上一点,EC⊥FA,ED⊥FB,垂足分别为C、D.求证:FE是CD的垂直平分线.
已知:E是∠AFB的平分线上一点,EC⊥FA,ED⊥FB,垂足分别为C、D.求证:FE是CD的垂直平分线.
分析 根据角平分线的性质得到EC=ED,根据全等三角形的性质得到FD=FC,根据线段垂直平分线的判定定理证明即可.
解答 证明:∵E是∠AFB的平分线上一点,EC⊥FA,ED⊥FB,
∴EC=ED,
在△FDE和△FCE中,
$\left\{\begin{array}{l}{∠DFE=∠CFE}\\{∠FDE=∠FCE}\\{FE=FE}\end{array}\right.$,
∴△FDE≌△FCE,
∴FD=FC,又EC=ED,
∴FE是CD的垂直平分线.
点评 本题考查的是线段垂直平分线的判定、角平分线的性质、全等三角形的判定和性质,掌握到线段的两个端点的距离相等在线段的垂直平分线上是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.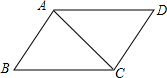 如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )
如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )
 如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )
如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )| A. | SSS | B. | SAS | C. | ASA | D. | HL |
2.下列多项式中,不能用公式法分解因式的是( )
| A. | -a2+b2 | B. | m2+2mn+2n2 | C. | x2+4xy+4y2 | D. | x2-$\frac{1}{2}$xy+$\frac{1}{16}$y2 |
3.如果x<0,那么x的立方根是( )
| A. | $\root{3}{x}$ | B. | $\sqrt{-x}$ | C. | -$\sqrt{x}$ | D. | ±$\root{3}{x}$ |
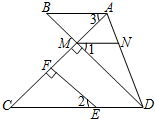 如图,已知EF⊥AC于点F,DB⊥AC于点M,∠1=∠2,∠3=∠C
如图,已知EF⊥AC于点F,DB⊥AC于点M,∠1=∠2,∠3=∠C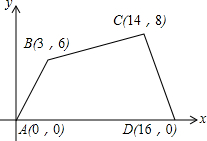 如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),
如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),