题目内容
14.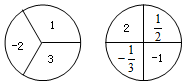 如图,甲转盘被分成 3 个面积相等的扇形,乙转盘被分成 4 个面积相等的扇形,每一个扇形都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转,直到指针指向一个区域为止).
如图,甲转盘被分成 3 个面积相等的扇形,乙转盘被分成 4 个面积相等的扇形,每一个扇形都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转,直到指针指向一个区域为止).(1)请你用画树状图或列表格的方法,求点(x,y)落在第二象限内的概率;
(2)直接写出点(x,y)落在函数y=-$\frac{1}{x}$图象上的概率.
分析 (1)通过树状图,列举出所有情况,再计算概率即可.
(2)然后再求得点(x,y)落在函数 y=-$\frac{1}{x}$图象上的情况,求其比值即可求得答案.
解答 解:(1)根据题意,画树状图: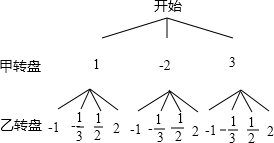
由上图可知,点(x,y)的坐标共有12种等可能的结果:
(1,-1),(1,-$\frac{1}{3}$),(1,$\frac{1}{2}$)(1,2),(-2,-1),(-2,-$\frac{1}{3}$)
(-2,$\frac{1}{2}$),(-2,2),(3,-1),(3,-$\frac{1}{3}$),(3,$\frac{1}{2}$),(3,2);
其中点(x,y)落在第二象限的共有2种:(-2,$\frac{1}{2}$),(-2,2),
所以,P(x,y)落在第二象限=$\frac{2}{12}$=$\frac{1}{6}$;
(2)点(x,y)落在函数y=-$\frac{1}{x}$的图象上共有三种情形(1,-1),(-2,$\frac{1}{2}$),(3,-$\frac{1}{3}$),
∴点(x,y)落在函数y=-$\frac{1}{x}$图象上的概率=$\frac{3}{12}$=$\frac{1}{4}$.
点评 本题考查列表法或树状图求概率,用到的知识点为:概率=所求情况数与总情况数之比,解题的关键是画出树状图,确定所求情况数与总情况数,属于基础题,中考常考题型.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
9.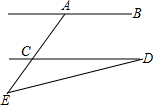 如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )
如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )
 如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )
如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )| A. | 24° | B. | 26° | C. | 34° | D. | 22° |
8.函数y=$\frac{\sqrt{x-2}}{x+4}$中,自变量x的取值范围是( )
| A. | x>4 | B. | x≥2 | C. | x≥2且x≠-4 | D. | x≠-4 |
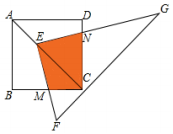 如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF,EG分别交BC,DC于点M,N,若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为$\frac{4}{9}$a2.
如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF,EG分别交BC,DC于点M,N,若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为$\frac{4}{9}$a2. 如图,△ABC中,DE∥BC,则$\frac{AB}{()}$=$\frac{()}{()}$.
如图,△ABC中,DE∥BC,则$\frac{AB}{()}$=$\frac{()}{()}$.