题目内容
10.小刚和小李做了一个游戏.如图,准备了一只碗,从侧面观察碗身是一条抛物线,而俯视图又是一个圆.已知碗深为5cm,碗口宽为10cm.(1)根据图中建立的坐标系,求出抛物线的关系式.
(2)小刚向碗中加水,使它刚好漂浮两张半径为2cm的圆形薄纸片;小李向碗中加水,使它刚好漂浮一张面积为4cm的正十二边形薄纸片,那么谁加入的水更多一些?
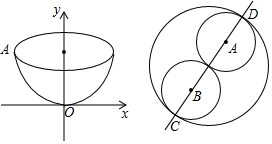
分析 (1)由图中的坐标系得到A(-5,5),代入y=ax2,得到a=$\frac{1}{5}$,于是得到结论;
(2)求得小刚向碗中加水的水深为$\frac{16}{5}$cm,小李向碗中加的水深为$\frac{4}{15}$cm,于是得到结论.
解答 解:(1)由图中的坐标系得:
∵碗深为5cm,碗口宽为10cm,
∴A(-5,5),
设抛物线解析式为:y=ax2,则5=25a,
解得:a=$\frac{1}{5}$,
∴抛物线的关系式为:y=$\frac{1}{5}$x2;
(2)∵小刚向碗中加水,使它刚好漂浮两张半径为2cm的圆形薄纸片;
∴水面圆的半径的4cm,
把x=4代入y=$\frac{1}{5}$x2得y=$\frac{16}{5}$,
∴小刚向碗中加水的水深为$\frac{16}{5}$cm,
∵小李向碗中加水,使它刚好漂浮一张面积为4cm的正十二边形薄纸片,
∴设正十二边形的外接圆的半径为r,
∴12×$\frac{1}{2}$r2•sin30°=4,
∴r=$\frac{2\sqrt{3}}{3}$,
∴把x=$\frac{2\sqrt{3}}{3}$代入y=$\frac{1}{5}$x2得y=$\frac{4}{15}$,
∴小李向碗中加的水深为$\frac{4}{15}$cm,
∴小刚向碗中加的水深.
点评 此题主要考查了二次函数的应用以及相切两圆的性质等知识,正确的理解题意是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.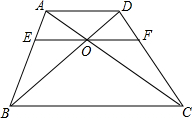 如图,四边形ABCD,AD∥BC,AD=m,BC=n,EF∥AD,经过点O,求EF的长为( )
如图,四边形ABCD,AD∥BC,AD=m,BC=n,EF∥AD,经过点O,求EF的长为( )
 如图,四边形ABCD,AD∥BC,AD=m,BC=n,EF∥AD,经过点O,求EF的长为( )
如图,四边形ABCD,AD∥BC,AD=m,BC=n,EF∥AD,经过点O,求EF的长为( )| A. | $\frac{m+n}{mn}$ | B. | $\frac{2mn}{m+n}$ | C. | $\frac{mn}{m+n}$ | D. | $\frac{m+n}{2mn}$ |
19.近似数1.20万精确到( )
| A. | 十分位 | B. | 百分位 | C. | 百位 | D. | 千位 |
 如图,AB、BC是⊙O的弦,OM∥BC交AB于M,若∠AOC=100°,则∠AMO=50°.
如图,AB、BC是⊙O的弦,OM∥BC交AB于M,若∠AOC=100°,则∠AMO=50°.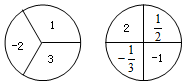 如图,甲转盘被分成 3 个面积相等的扇形,乙转盘被分成 4 个面积相等的扇形,每一个扇形都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转,直到指针指向一个区域为止).
如图,甲转盘被分成 3 个面积相等的扇形,乙转盘被分成 4 个面积相等的扇形,每一个扇形都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转,直到指针指向一个区域为止). 如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=$4\sqrt{3}$,∠BAD=60°,且AB>$4\sqrt{3}$.给出下列结论:
如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=$4\sqrt{3}$,∠BAD=60°,且AB>$4\sqrt{3}$.给出下列结论: