题目内容
8.函数y=$\frac{\sqrt{x-2}}{x+4}$中,自变量x的取值范围是( )| A. | x>4 | B. | x≥2 | C. | x≥2且x≠-4 | D. | x≠-4 |
分析 根据分式和二次根式有意义的条件进行选择即可.
解答 解:由题意得$\left\{\begin{array}{l}{x-2≥0}\\{x+4≠0}\end{array}\right.$,
解得x≥2,x≠-4,
∴自变量x的取值范围是x≥2,
故选B.
点评 本题考查了函数自变量的取值范围问题,掌握分式和二次根式有意义的条件是解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
19.近似数1.20万精确到( )
| A. | 十分位 | B. | 百分位 | C. | 百位 | D. | 千位 |
17.每天供给地球光和热的太阳与我们的距离非常遥远,它距地球的距离约为15000000千米,将150000000千米用科学记数法表示为( )
| A. | 0.15×109千米 | B. | 1.5×108千米 | C. | 15×107千米 | D. | 1.5×107千米 |
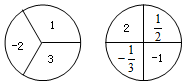 如图,甲转盘被分成 3 个面积相等的扇形,乙转盘被分成 4 个面积相等的扇形,每一个扇形都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转,直到指针指向一个区域为止).
如图,甲转盘被分成 3 个面积相等的扇形,乙转盘被分成 4 个面积相等的扇形,每一个扇形都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转,直到指针指向一个区域为止).