题目内容
9.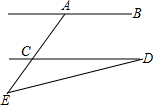 如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )
如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )| A. | 24° | B. | 26° | C. | 34° | D. | 22° |
分析 先根据平行线的性质得到∠ACD=180°-∠CAB=64°,然后根据三角形外角性质得∠D=∠ACD-∠E=24°.
解答 解:∵AB∥CD,∠CAB=116°,
∴∠ACD=180°-∠CAB=64°,
∵∠E=40°,
∴∠D=∠ACD-∠E=24°.
故选:A.
点评 本题考查了平行线性质,关键是熟悉两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等,同时考查了三角形外角性质.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
20.已知一次函数y1=kx+b(k<0)与反比例函数y2=$\frac{m}{x}$(m≠0)的图象相交于A、B两点,其横坐标分别是-1和3,当y1>y2,实数x的取值范围是( )
| A. | x<-1或0<x<3 | B. | -1<x<0或0<x<3 | C. | -1<x<0或x>3 | D. | 0<x<3 |
5.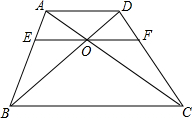 如图,四边形ABCD,AD∥BC,AD=m,BC=n,EF∥AD,经过点O,求EF的长为( )
如图,四边形ABCD,AD∥BC,AD=m,BC=n,EF∥AD,经过点O,求EF的长为( )
 如图,四边形ABCD,AD∥BC,AD=m,BC=n,EF∥AD,经过点O,求EF的长为( )
如图,四边形ABCD,AD∥BC,AD=m,BC=n,EF∥AD,经过点O,求EF的长为( )| A. | $\frac{m+n}{mn}$ | B. | $\frac{2mn}{m+n}$ | C. | $\frac{mn}{m+n}$ | D. | $\frac{m+n}{2mn}$ |
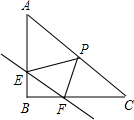 如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB=$\frac{6}{5}$,BC=$\frac{8}{5}$.
如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB=$\frac{6}{5}$,BC=$\frac{8}{5}$. 如图,AB、BC是⊙O的弦,OM∥BC交AB于M,若∠AOC=100°,则∠AMO=50°.
如图,AB、BC是⊙O的弦,OM∥BC交AB于M,若∠AOC=100°,则∠AMO=50°.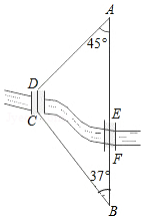 如图,A,B两地之间有条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.已知BC=11km,∠A=45°,∠B=37°,桥DC和AB平行,桥DC与桥EF的长相等.
如图,A,B两地之间有条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.已知BC=11km,∠A=45°,∠B=37°,桥DC和AB平行,桥DC与桥EF的长相等.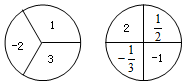 如图,甲转盘被分成 3 个面积相等的扇形,乙转盘被分成 4 个面积相等的扇形,每一个扇形都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转,直到指针指向一个区域为止).
如图,甲转盘被分成 3 个面积相等的扇形,乙转盘被分成 4 个面积相等的扇形,每一个扇形都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转,直到指针指向一个区域为止). 如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=$4\sqrt{3}$,∠BAD=60°,且AB>$4\sqrt{3}$.给出下列结论:
如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=$4\sqrt{3}$,∠BAD=60°,且AB>$4\sqrt{3}$.给出下列结论: