题目内容
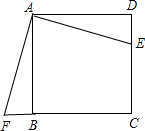 如图,E是正方形ABCD中CD边上任意一点,把△ADE绕A顺时针方向旋转一个角度后得到△ABF,则旋转的角度可能是( )
如图,E是正方形ABCD中CD边上任意一点,把△ADE绕A顺时针方向旋转一个角度后得到△ABF,则旋转的角度可能是( )| A、90° | B、45° |
| C、135° | D、270° |
考点:旋转的性质
专题:
分析:由四边形ABCD为正方形,得到AD=AB,∠DAB=90°,又△ADE绕点A顺时针旋转后与△ABF重合,则∠DAB等于旋转角,即可得到旋转的角度.
解答:解:∵四边形ABCD为正方形,
∴AD=AB,∠DAB=90°,
又∵△ADE绕点A顺时针旋转后与△ABF重合,
∴∠DAB等于旋转角,
∴旋转的角度是90°.
故选A.
∴AD=AB,∠DAB=90°,
又∵△ADE绕点A顺时针旋转后与△ABF重合,
∴∠DAB等于旋转角,
∴旋转的角度是90°.
故选A.
点评:本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了正方形的性质.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
若∠A=20°18′,∠B=20°15″,∠C=20.25°,则有( )
| A、∠A>∠B>∠C |
| B、∠B>∠A>∠C |
| C、∠A>∠C>∠B |
| D、∠C>∠A>∠B |
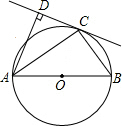 如图,AB是⊙O的直径,C是⊙O上一点,AD与过C点的切线互相垂直,垂足为D.
如图,AB是⊙O的直径,C是⊙O上一点,AD与过C点的切线互相垂直,垂足为D. 王刚将一副三角板如图所示摆在一起,若已知CD=2,AB=
王刚将一副三角板如图所示摆在一起,若已知CD=2,AB= 已知,如图,∠A=∠ACE,∠B=∠BDF,且∠A=∠B,求证:EC∥DF.
已知,如图,∠A=∠ACE,∠B=∠BDF,且∠A=∠B,求证:EC∥DF. 如图,OC平分∠AOB,如果∠AOB=36°,则∠AOC=
如图,OC平分∠AOB,如果∠AOB=36°,则∠AOC= 已知:如图,OB是∠AOC的角平分线,OC是∠AOD的角平分线,∠COD=70°,那么∠AOD的度数为
已知:如图,OB是∠AOC的角平分线,OC是∠AOD的角平分线,∠COD=70°,那么∠AOD的度数为