题目内容
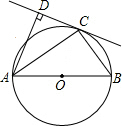 如图,AB是⊙O的直径,C是⊙O上一点,AD与过C点的切线互相垂直,垂足为D.
如图,AB是⊙O的直径,C是⊙O上一点,AD与过C点的切线互相垂直,垂足为D.(1)求证:AC平分∠DAB;
(2)连接BC,若AB=12cm,∠ABC=60°,求CD的长.
考点:切线的性质
专题:计算题
分析:(1)证明:连结OC,如图,根据切线的性质得OC⊥CD,而AD⊥CD,则AD∥OC,根据平行线的性质有∠2=∠3,加上∠1=∠3,所以∠1=∠2,因此可判断AC平分∠DAB;
(2)根据圆周角定理得∠ACB=90°,则利用含30度的直角三角形三边的关系可计算出BC=
AB=6,AC=
BC=6
,然后在Rt△ADC中计算出CD.
(2)根据圆周角定理得∠ACB=90°,则利用含30度的直角三角形三边的关系可计算出BC=
| 1 |
| 2 |
| 3 |
| 3 |
解答:(1)证明:连结OC,如图,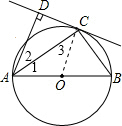
∵CD为⊙O的切线,
∴OC⊥CD,
∵AD⊥CD,
∴AD∥OC,
∴∠2=∠3,
∵OA=OC,
∴∠1=∠3,
∴∠1=∠2,
∴AC平分∠DAB;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=60°,
∴∠1=30°,
∴BC=
AB=6,
∴AC=
BC=6
,
在Rt△ADC中,∵∠2=∠1=30°,
∴CD=
AC=3
(cm).

∵CD为⊙O的切线,
∴OC⊥CD,
∵AD⊥CD,
∴AD∥OC,
∴∠2=∠3,
∵OA=OC,
∴∠1=∠3,
∴∠1=∠2,
∴AC平分∠DAB;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=60°,
∴∠1=30°,
∴BC=
| 1 |
| 2 |
∴AC=
| 3 |
| 3 |
在Rt△ADC中,∵∠2=∠1=30°,
∴CD=
| 1 |
| 2 |
| 3 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了平行线的判定与性质和含30度的直角三角形三边的关系.

练习册系列答案
相关题目
 如图,一场暴雨过后,垂直于地面的一棵树在距地面2m处折断,树尖B恰好碰到地面,经测量AB=4m,则树高为( )
如图,一场暴雨过后,垂直于地面的一棵树在距地面2m处折断,树尖B恰好碰到地面,经测量AB=4m,则树高为( )A、2
| ||
B、2
| ||
C、(2
| ||
| D、4m |
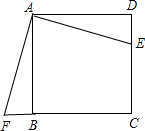 如图,E是正方形ABCD中CD边上任意一点,把△ADE绕A顺时针方向旋转一个角度后得到△ABF,则旋转的角度可能是( )
如图,E是正方形ABCD中CD边上任意一点,把△ADE绕A顺时针方向旋转一个角度后得到△ABF,则旋转的角度可能是( )| A、90° | B、45° |
| C、135° | D、270° |
 如图所示,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,它的左视图是( )
如图所示,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,它的左视图是( )



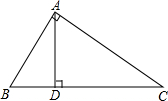 在△ABC中,∠BAC=90°,AD⊥BC于点D,若AB=30cm,BC=50cm,求线段CD的长.
在△ABC中,∠BAC=90°,AD⊥BC于点D,若AB=30cm,BC=50cm,求线段CD的长.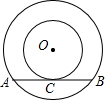 半径为5的大⊙O的弦与小⊙O相切于点C,且AB=8,则小⊙O的半径为
半径为5的大⊙O的弦与小⊙O相切于点C,且AB=8,则小⊙O的半径为