题目内容
1.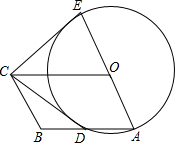 如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:(1)求证:CD是⊙O的切线;
(2)若平行四边形0ABC的两边长是方程x2-16x+60=0的两根,求平行四边形OABC的面积.
分析 (1)连接OD,证出△EOC≌△DOC,推出∠ODC=∠OEC=90°,根据切线的判定推出即可;
(2)解方程求出OC和OA,然后根据勾股定理求出CD,根据三角形的面积公式求出DF,根据平行四边形的面积公式求出即可.
解答 (1)证明:∵CE是⊙O的切线,
∴∠OEC=90°, 如图1,连接OD,
如图1,连接OD,
∵四边形OABC是平行四边形,
∴AO=BC,OC=AB,OC∥AB,
∴∠EOC=∠A,∠COD=∠ODA,
∵OD=OA,
∴∠A=∠ODA,
∴∠EOC=∠DOC,
在△EOC和△DOC中,
$\left\{\begin{array}{l}{OE=OD}\\{∠EOC=∠DOC}\\{OC=OC}\end{array}\right.$,
∴△EOC≌△DOC(SAS),
∴∠ODC=∠OEC=90°,
∴OD⊥CD,
∴CD是⊙O的切线;
(2)解:∵平行四边形0ABC的两边长是方程x2-16x+60=0的两根, 解方程x2-16x+60=0得,x1=10,x2=6,
解方程x2-16x+60=0得,x1=10,x2=6,
∴OC=10,OA=6,
过D作DF⊥OC于F,如图2,
在Rt△CDO中,OC=10,OD=OA=6,由勾股定理得:CD=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
由三角形的面积公式得:$\frac{1}{2}$×CD×OD=$\frac{1}{2}$×OC×DF,
∴DF=$\frac{CD×OD}{OC}$=$\frac{8×6}{10}$=4.8,
∴平行四边形OABC的面积是OC×DF=10×4.8=48.
点评 本题考查了切线的性质和判定,解一元二次方程,平行四边形的性质,平行线的性质,勾股定理,三角形的面积的应用,主要考查学生综合运用性质进行推理和计算的能力.

练习册系列答案
相关题目

 已知线段AB.
已知线段AB.