题目内容
5.如图(1),沿平行四边形ABCD的对角线AC剪开,得到△ABC1和△ADC2,并将△ADC2绕点A旋转至AC2∥BC1(如图(2)).(1)求证:AC2平分∠C1AD;
(2)若AC1∥DC2,问图(1)中的四边形ABCD是何种特殊的平行四边形?并说明理由.

分析 (1)由平行四边形的性质得出△ABC1≌△ADC2,得出∠BC1 A=∠DAC2,由平行线的性质得出∠BC1 A=∠C1A C2,证出∠DAC2=∠C1 A C2即可;
(2)由平行线的性质得出∠C1 AC2=∠AC2 D,由∠DAC2=∠C1 A C2,得出∠AC2 D=∠C2 AD,证出AD=C2 D,由平行四边形的性质得出C2 D=AB,得出AD=AB,即可得出结论.
解答 (1)证明:由平行四边形的性质得:△ABC1≌△ADC2,
∴∠BC1 A=∠DAC2,
∵AC2∥BC1,
∴∠BC1 A=∠C1A C2,
∴∠DAC2=∠C1 A C2,
∴AC2平分∠C1AD;
(2)解:图(1)中的四边形ABCD是菱形;理由如下:
∵AC1∥DC2,
∴∠C1 AC2=∠AC2 D,
∵∠DAC2=∠C1 A C2,
∴∠AC2 D=∠C2 AD,
∴AD=C2 D,
∵C2 D=AB,
∴AD=AB,
∴图(1)中的四边形ABCD是菱形.
点评 本题考查了旋转的性质、平行四边形的性质、菱形的判定、平行线的性质、等腰三角形的判定等知识;熟练掌握平行四边形的性质,弄清角之间的关系是解决问题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目

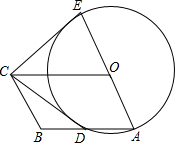 如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
 如图所示,线段AB=2.8m,点C分AB为AC和BC的比为2:$\frac{4}{5}$,D为AB中点,求CD的长.
如图所示,线段AB=2.8m,点C分AB为AC和BC的比为2:$\frac{4}{5}$,D为AB中点,求CD的长. 如图,在△ABC中,AB=AC=2,∠B=75°,则点B到边AC的距离为1.
如图,在△ABC中,AB=AC=2,∠B=75°,则点B到边AC的距离为1.