题目内容
9.将方程x2-2x+1=4-3x化为一般形式为x2+x-3=0,其中a=1,b=1,c=-3,方程的根为x1=$\frac{-1+\sqrt{13}}{2}$,x2=$\frac{-1-\sqrt{13}}{2}$.分析 要确定一次项系数和常数项,首先要把方程化成一般形式.
解答 解:x2-2x+1=4-3x化为一般形式为x2+x-3=0,
a=1,b=1,c=-3,
方程的根为x1=$\frac{-1+\sqrt{13}}{2}$,x2=$\frac{-1-\sqrt{13}}{2}$.
故答案为:x2+x-3=0,1,1,-3,x1=$\frac{-1+\sqrt{13}}{2}$,x2=$\frac{-1-\sqrt{13}}{2}$.
点评 本题考查了一元二次方程的一般形式,一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.

练习册系列答案
相关题目
19.用配方法解方程x2-4x+1=0,下列配方正确是( )
| A. | (x-2)2=5 | B. | (x+2)2=5 | C. | (x-2)2=3 | D. | (x+2)2=5 |
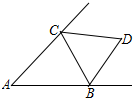 如图,△ABC的两条外角平分线CD、BD交于点D,若∠D=68°,则∠A=44°.
如图,△ABC的两条外角平分线CD、BD交于点D,若∠D=68°,则∠A=44°.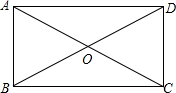 如图,矩形ABCD中,AC、BD交于点O,请你添加一个条件,使矩形ABCD成为正方形,你添加的条件是AB=BC(答案不唯一,如AC⊥BD等).
如图,矩形ABCD中,AC、BD交于点O,请你添加一个条件,使矩形ABCD成为正方形,你添加的条件是AB=BC(答案不唯一,如AC⊥BD等).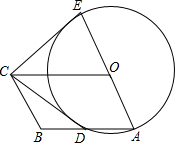 如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
 如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,得到线段AB,则线段AB的中点E的坐标为(7,4).
如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,得到线段AB,则线段AB的中点E的坐标为(7,4).