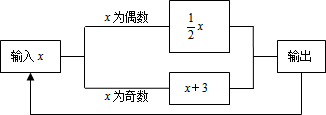
题目内容
16.等腰△ABC中,AB=AC=5,BC=8,则底角∠B的正切值是$\frac{3}{4}$.分析 根据题意先画出图形,过A点作AD⊥BC交BC于点D,根据等腰三角形的性质求出BD,再根据勾股定理求出AD,最后根据∠B的正切值是$\frac{AD}{BD}$,代入计算即可.
解答 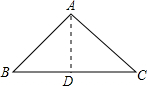 解:如图:过A点作AD⊥BC交BC于点D,
解:如图:过A点作AD⊥BC交BC于点D,
∵AB=AC=5,BC=8,
∴BD=CD=4,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴∠B的正切值是$\frac{AD}{BD}$=$\frac{3}{4}$;
故答案为:$\frac{3}{4}$.
点评 此题考查了解直角三角形,用到的知识点勾股定理、锐角三角函数、等腰三角形的性质,关键是根据题意画出图形,构造直角三角形.

练习册系列答案
相关题目
6.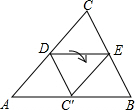 如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D等于( )
如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D等于( )
 如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D等于( )
如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D等于( )| A. | 35° | B. | 55° | C. | 70° | D. | 110° |
11.前岐“四季柚”是福鼎市著名特产,产品畅销省内外,现有一个产品销售点在经销时发现:如果每箱产品盈利10元,每天可售出50箱;若每箱产品每涨价1元,日销售量将减少2箱;据此规律,要使每天的盈利达到600元,设每箱产品涨价x元,则列出关于x的方程是( )
| A. | (10-x)(50-2x)=600 | B. | (10+x)(50+2x)=600 | C. | (10-x)(50+2x)=600 | D. | (10+x)(50-2x)=600 |
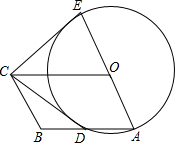 如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题: 如图所示,线段AB=2.8m,点C分AB为AC和BC的比为2:$\frac{4}{5}$,D为AB中点,求CD的长.
如图所示,线段AB=2.8m,点C分AB为AC和BC的比为2:$\frac{4}{5}$,D为AB中点,求CD的长.