题目内容
方程组
的解是 .
|
考点:高次方程
专题:
分析:先把x2-2xy+x=0转化成2y=1+x,再代入x2-4y2=1中,求出x的值,再代入2y=1+x中,即可求出y的值,即可求出方程组的解.
解答:解:
,
由②得:x=2xy-x2,
即2y=1+x,③
把③代入①得:x2-(1+x)2=1,
解得:x=-1,
把x=-1代入③得:y=0,
所以方程组
的解是:
;
故答案为:
.
|
由②得:x=2xy-x2,
即2y=1+x,③
把③代入①得:x2-(1+x)2=1,
解得:x=-1,
把x=-1代入③得:y=0,
所以方程组
|
|
故答案为:
|
点评:此题考查了高次方程,解题的关键是把x2-2xy+x=0转化成2y=1+x,再代入即可,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,AB=CD.P是BC延长线上的一点,PE∥AB交AC延长线于E,
如图,在梯形ABCD中,AD∥BC,AB=CD.P是BC延长线上的一点,PE∥AB交AC延长线于E,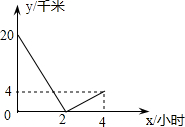 甲、乙二人从A、B两地同时出发相向而行,相遇后,甲立即返回,先于乙回到A地,两人相距的路程y(千米)与行驶时间x(小时)之间的函数关系如图所示,则乙从B地到A地需时间
甲、乙二人从A、B两地同时出发相向而行,相遇后,甲立即返回,先于乙回到A地,两人相距的路程y(千米)与行驶时间x(小时)之间的函数关系如图所示,则乙从B地到A地需时间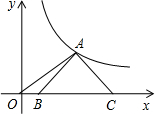 如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数
如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数  小红制作了一个对面图案均相同的正方体礼品盒,(如图所示),则这们礼品盒的平面展开图是( )
小红制作了一个对面图案均相同的正方体礼品盒,(如图所示),则这们礼品盒的平面展开图是( )



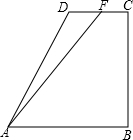 如图,直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=BC,且CD=
如图,直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=BC,且CD=