题目内容
如图，在梯形ABCD中，AD∥BC，AB=CD．P是BC延长线上的一点，PE∥AB交AC延长线于E，PF∥CD交BD延长线于F．若PE=2，PF=7，则AB的长为（ ）
| A、3 | B、4 | C、5 | D、6 |
考点：相似三角形的判定与性质,等腰梯形的性质
专题：计算题
分析：先设AB=x，由于PE∥AB，利用平行线分线段成比例定理的推论可得△PEC∽△BAC，从而有AB：PE=BC：CP，即x：2=BC：CP，同理可得x：7=BC：BP，利用比例性质可化为
=
，两式联合可得
=
，解即可．
| 7-x |
| x |
| CP |
| BC |
| 7-x |
| x |
| 2 |
| x |
解答：解：如右图，设AB=x，
∵PE∥AB，
∴△PEC∽△BAC，
∴AB：PE=BC：CP，
即x：2=BC：CP，
同理可得△BCD∽△BPF，
∴DC：PF=BC：BP，
∵AB=CD，
∴x：7=BC：BP，
∴
=
，
∴
=
，
解得x=5（0舍去）．
故选C．
如右图，设AB=x，∵PE∥AB，
∴△PEC∽△BAC，
∴AB：PE=BC：CP，
即x：2=BC：CP，
同理可得△BCD∽△BPF，
∴DC：PF=BC：BP，
∵AB=CD，
∴x：7=BC：BP，
∴
| 7-x |
| x |
| CP |
| BC |
∴
| 7-x |
| x |
| 2 |
| x |
解得x=5（0舍去）．
故选C．
点评：本题考查了平行线分线段成比例定理的推论、相似三角形的判定和性质，解题的关键是利用比例性质求出
=
．
| 7-x |
| x |
| CP |
| BC |
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
从一副扑克的所有黑桃牌中随机抽出一张扑克牌，恰好是黑桃9的概率是（ ）
| A、0 | ||
B、
| ||
C、
| ||
D、
|
如图，在4×4的正方形网格中，cosα=（ ）A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
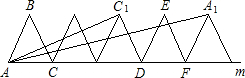如图，已知边长为2的正三角形ABC沿直线m滚动，当△ABC滚动一周时，到△DEF位置．设△ABC滚动240°时，点C的位置为C1，△ABC滚动480°时，点A的位置为点A1．根据三角函数正切的两角和公式
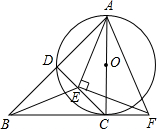如图，等腰Rt△ABC中，AC=BC，以AC为直径作⊙O交AB于D点，E为CD上的一个动点，过E作AE的垂线交BC的延长线于点F，连接AE、BE、EF，下列结论：