Question

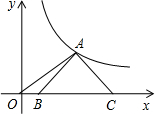如图，等腰Rt△ABC的斜边BC在x轴上，顶点A在反比例函数 y=

3

x

（x＞0）的图象上，连接OA．则OC²-OA²的值为（　　）

• A、7
• B、6
• C、3
• D、4

Answer 1

考点：反比例函数综合题

专题：

分析：首先根据等腰直角三角形的性质得出AD=CD=BD，进而求出OC²-OA²=2DO•AD，利用顶点A在反比例函数 y=

3

x

（x＞0）的图象上，得出xy=3，即可得出答案．

解答：解：过点A作AD⊥OC于点D，
∵△ABC是等腰Rt△ABC，AD⊥BC，
∴AD=CD=BD，
∵在Rt△AOD中，AD²+OD²=OA²，
∴OD²=OA²-AD²，
∵OC²-OA²=（OD+DC）²-OA²=OD²-OA²+DC²+2DO•CD，
=OA²-AD²-OA²+DC²+2DO•CD，
=2DO•CD，
=2DO•AD，
∵顶点A在反比例函数 y=

3

x

（x＞0）的图象上，
∴xy=3，
∴OC²-OA²=2DO•AD=2×3=6．
故选B．

点评：此题主要考查了反比例函数的综合应用以及等腰直角三角形的性质，根据已知得出OC²-OA²=2DO•AD是解题关键．