题目内容
已知⊙O的半径为5,OP=4,那么经过点P,且长为整数的弦共有 条.
考点:垂径定理,勾股定理
专题:探究型
分析:过点P最长的弦是10,根据已知条件,可以求出过点P的最短的弦是6,故过点P的弦的长度在6和10之间,所以过点P的弦中长度为整数的弦的条数为8.
解答: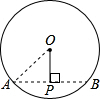 解:如图示,作AB⊥OP于P,则AP=BP,
解:如图示,作AB⊥OP于P,则AP=BP,
在Rt△AOP中,
∵OP=4,OA=5,
∴AP=3,
∴AB=6,
∴过点P的弦的长度在6和10之间,且过P点的弦中长度为9,8,7的分别有两条,长度是6,10的各一条,
∴过点P的弦中长度为整数的弦的条数为8.
故答案为:8.
 解:如图示,作AB⊥OP于P,则AP=BP,
解:如图示,作AB⊥OP于P,则AP=BP,在Rt△AOP中,
∵OP=4,OA=5,
∴AP=3,
∴AB=6,
∴过点P的弦的长度在6和10之间,且过P点的弦中长度为9,8,7的分别有两条,长度是6,10的各一条,
∴过点P的弦中长度为整数的弦的条数为8.
故答案为:8.
点评:本题主要考查了垂径定理,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形再根据勾股定理求解.

练习册系列答案
相关题目
设m,n是方程x2-x-2012=0的两个实数根,则m2+n的值为( )
| A、1006 | B、2011 |
| C、2012 | D、2013 |
有五张背面相同,正面分别写有数据:
,
,
,π,-2的纸牌.充分洗匀后,从中随机抽取一张,抽到无理数的概率为( )
| 1 |
| 3 |
| 2 |
| 3 |
| A、20% | B、40% |
| C、60% | D、80% |
 如图,有两个半径差1的圆,它们各有一个内接正八边形.已知阴影部分的面积是4
如图,有两个半径差1的圆,它们各有一个内接正八边形.已知阴影部分的面积是4| 2 |
A、
| ||
| B、3 | ||
| C、2 | ||
D、
|