题目内容
5.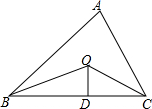 如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于,且OD=4,△ABC的面积是( )
如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于,且OD=4,△ABC的面积是( )| A. | 25 | B. | 84 | C. | 42 | D. | 21 |
分析 连接OA,作OE⊥AB于E,OF⊥AC于F,如图,利用角平分线的性质得到OD=OE=OF=4,然后根据三角形面积公式得到△ABC的面积=S△AOB+S△BOC+S△AOC=$\frac{1}{2}$×4×(AB+BC+AC),再把三角形的周长代入计算即可.
解答 解:连接OA,作OE⊥AB于E,OF⊥AC于F,如图,
∵OB,OC分别平分∠ABC和∠ACB,
∴OD=OE=4,OD=OF=4,
∴△ABC的面积=
S△AOB+S△BOC+S△AOC
=$\frac{1}{2}$•OE•AB+$\frac{1}{2}$•OD•BC+$\frac{1}{2}$•OF•AC
=$\frac{1}{2}$×4×(AB+BC+AC)
=$\frac{1}{2}$×4×21
=42.
故选C.
点评 本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.这里的距离是指点到角的两边垂线段的长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13. 如图所示,△ACE≌△DBF,AE∥DF,AD=6,BC=2,则AB的长度等于( )
如图所示,△ACE≌△DBF,AE∥DF,AD=6,BC=2,则AB的长度等于( )
 如图所示,△ACE≌△DBF,AE∥DF,AD=6,BC=2,则AB的长度等于( )
如图所示,△ACE≌△DBF,AE∥DF,AD=6,BC=2,则AB的长度等于( )| A. | 2 | B. | 8 | C. | 6 | D. | 3 |
10.如果xm=4,xn=8(m、n为自然数),那么x3m-n等于( )
| A. | $\frac{3}{2}$ | B. | 4 | C. | 8 | D. | 56 |
17.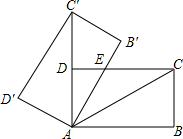 如图,将矩形ABCD绕点A旋转至矩形AB'C'D'位置,此时AC'的中点恰好与D点重合,AB'交CD于点E,若AD=3,则△AEC的面积为( )
如图,将矩形ABCD绕点A旋转至矩形AB'C'D'位置,此时AC'的中点恰好与D点重合,AB'交CD于点E,若AD=3,则△AEC的面积为( )
 如图,将矩形ABCD绕点A旋转至矩形AB'C'D'位置,此时AC'的中点恰好与D点重合,AB'交CD于点E,若AD=3,则△AEC的面积为( )
如图,将矩形ABCD绕点A旋转至矩形AB'C'D'位置,此时AC'的中点恰好与D点重合,AB'交CD于点E,若AD=3,则△AEC的面积为( )| A. | 12 | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6 |
15.下列各式中,正确的是( )
| A. | |-$\frac{6}{7}$|<|-$\frac{1}{6}$| | B. | -$\frac{5}{8}$>-0.618 | ||
| C. | (-2)100<(-3)101 | D. | -$\frac{1998}{1999}$<-$\frac{1997}{1998}$ |
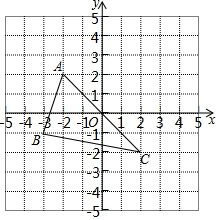 如图,△ABC的顶点坐标分别为A(-2,2),B(-3,-1),C(2,-2).
如图,△ABC的顶点坐标分别为A(-2,2),B(-3,-1),C(2,-2). 一个几何体从正面看到的图形如图所示,它可以由三角尺绕直线1旋转一周而成的是( )
一个几何体从正面看到的图形如图所示,它可以由三角尺绕直线1旋转一周而成的是( )


