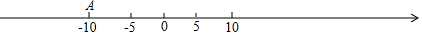��Ŀ����
20�����õķֽ���ʽ�ķ�������ȡ����ʽ������ʽ�������и���Ķ���ʽֻ���������������ֽ⣬��x2-4y2-2x+4y������ϸ�Ĺ۲����ʽ�Ӿͻᷢ�֣�ǰ�������ƽ���ʽ�����������ȡ����ʽ��ǰ�������ֱַ�ֽ���ʽ����������ʽ��Ȼ����ȡ����ʽ�Ϳ����������ʽ�ӵķֽ���ʽ�ˣ�����Ϊ��x2-4y2-2x+4y=��x+2y����x-2y��-2��x-2y��=��x-2y����x+2y-2�������ַֽ���ʽ�ķ����з���ֽⷨ���������ַ�������������⣮��1���ֽ���ʽ��x2+2xy+y2��
��2���ֽ���ʽ��a2-9-2ab+b2��
��3����ABC����a��b��c����a2-4bc+4ac-ab=0���жϡ�ABC����״��
���� ��1��������ȫƽ����ʽ�ֽ�ó����ɣ�
��2�����Ƚ���һ������������ϣ�������ȫƽ����ʽ�ֽ���ʽ����������ƽ���ʽ�ֽ���ʽ�ó����ɣ�
��3�����Ƚ���һ�������Լ��ڶ���������ϣ�������ȡ����ʽ���ֽ���ʽ�����ɵó�a��b��c�Ĺ�ϵ���ж���������״���ɣ�
��� �⣺��1��x2+2xy+y2=��x+y��2��
��2��a2-9-2ab+b2
=��a-b��2-32
=��a-b+3����a-b-3����
��3����a2-4bc+4ac-ab=0��
a2-ab+4ac-4bc=0��
��a��a-b��+4c��a-b��=0��
�ࣨa-b����a+4c��=0��
��a+4c��0��
��a-b=0��
��a=b��
���ABC����״�ǵ��������Σ�
���� ������Ҫ�����˷���ֽⷨ�ֽ���ʽ�Լ����������ε��ж�����ȷ����ֽ�ó��ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
11����������������3ǧ�˼�Ϊ+3�������ȱ�˧˧��3ǧ�˼�Ϊ��������
| A�� | +3 | B�� | 0 | C�� | -3 | D�� | -6 |
15����ϰ�У�С��ͬѧ��������4����ʽ�ֽ��⣬����ΪС��������ȷ���У�������
��x3+x=x��x+1����x-1����
��x2-2xy+y2=��x-y��2��
��a2-a+1=a��a-1��+1��
��x2-16y2=��x+4y����x-4y����
��x3+x=x��x+1����x-1����
��x2-2xy+y2=��x-y��2��
��a2-a+1=a��a-1��+1��
��x2-16y2=��x+4y����x-4y����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
5��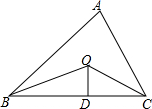 ��ͼ����֪��ABC���ܳ���21��OB��OC�ֱ�ƽ�֡�ABC�͡�ACB��OD��BC�ڣ���OD=4����ABC������ǣ�������
��ͼ����֪��ABC���ܳ���21��OB��OC�ֱ�ƽ�֡�ABC�͡�ACB��OD��BC�ڣ���OD=4����ABC������ǣ�������
 ��ͼ����֪��ABC���ܳ���21��OB��OC�ֱ�ƽ�֡�ABC�͡�ACB��OD��BC�ڣ���OD=4����ABC������ǣ�������
��ͼ����֪��ABC���ܳ���21��OB��OC�ֱ�ƽ�֡�ABC�͡�ACB��OD��BC�ڣ���OD=4����ABC������ǣ�������| A�� | 25 | B�� | 84 | C�� | 42 | D�� | 21 |
9�����a��b�������в���ʽ�г������ǣ�������
| A�� | a-3��b-3 | B�� | 3-a��3-b | C�� | $\frac{1}{3}$a��$\frac{1}{3}$b | D�� | -2a��-2b |
 �ס����������ò�ͬ�Ľ�ͨ���ߣ���ͬһ·�ߴ�A�س���ǰ��B�أ��׳���1h���ҳ��������˵���B�غ����̰�ԭ�ٶȷ��أ������A�����y����km��������A�����y����km�������뿪A�ص�ʱ��Ϊx��h����y����y����x֮��ĺ���ͼ����ͼ��ʾ��
�ס����������ò�ͬ�Ľ�ͨ���ߣ���ͬһ·�ߴ�A�س���ǰ��B�أ��׳���1h���ҳ��������˵���B�غ����̰�ԭ�ٶȷ��أ������A�����y����km��������A�����y����km�������뿪A�ص�ʱ��Ϊx��h����y����y����x֮��ĺ���ͼ����ͼ��ʾ��