题目内容
14.甲列车从A地开往B地,速度是60千米/小时,15分钟后,乙列车从B地开往A地,速度是90千米/小时,已知A,B两地相距225千米,两车相遇的地方离A地多远?分析 设乙车行驶x小时后与甲车相遇,根据题意可得等量关系:甲车行驶的距离+乙车x小时行驶的距离=225千米,根据等量关系,列出方程即可.
解答 解:设乙车行驶x小时后与甲车相遇,根据题意得:
60×$\frac{15}{60}$+(60+90)x=225,
解得:x=1.4,
60×$\frac{15}{60}$+60×1.4=99(千米),
答:两车相遇的地方距离A地99千米.
点评 此题考查了一元一次方程的应用,关键是正确理解题意,找出等量关系,设出未知数,列出方程.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
5.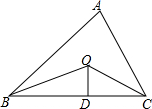 如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于,且OD=4,△ABC的面积是( )
如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于,且OD=4,△ABC的面积是( )
 如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于,且OD=4,△ABC的面积是( )
如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于,且OD=4,△ABC的面积是( )| A. | 25 | B. | 84 | C. | 42 | D. | 21 |
2.某餐厅共有10名员工,所有员工的工资情况如下表:
则该餐厅所有员工工资的众数、中位数分别是( )
| 人员 | 经理 | 厨师 | 会计 | 保安 | 服务员 |
| 人数(人) | 1 | 2 | 1 | 1 | 5 |
| 工资(元) | 5000 | 4000 | 3500 | 3000 | 2000 |
| A. | 5000,3500 | B. | 5000,2500 | C. | 2000,3500 | D. | 2000,2500 |
9.如果a>b,则下列不等式中成立的是( )
| A. | a-3<b-3 | B. | 3-a<3-b | C. | $\frac{1}{3}$a<$\frac{1}{3}$b | D. | -2a>-2b |
6.若x2+2xy+y2=(x-y)2-A,则A为( )
| A. | 2xy | B. | -2xy | C. | -4xy | D. | 4xy |
4.如图,有5张扑克牌,从中随机抽取一张牌,点数是偶数的可能性大小是( )


| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
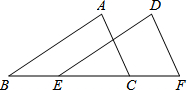 如图,△ABC≌△DEF,∠A和∠D是对应角,AB和DE是对应边,那么还有对应角是∠B=∠E,∠C=∠F,对应边是BC=EF,AC=DF.
如图,△ABC≌△DEF,∠A和∠D是对应角,AB和DE是对应边,那么还有对应角是∠B=∠E,∠C=∠F,对应边是BC=EF,AC=DF.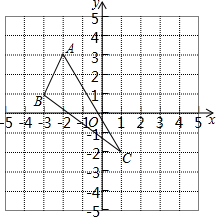 如图,
如图,