题目内容
17．求适合$\frac{7}{3}$+2x＜8-$\frac{x}{4}$及$\frac{4}{5}$-6x＜$\frac{1}{3}$-$\frac{x}{5}$的x值的范围．分析 求出两个不等式的解集，再求其公共解．
解答 解：解不等式$\frac{7}{3}$+2x＜8-$\frac{x}{4}$，得x＜$\frac{68}{27}$；
解不等式$\frac{4}{5}$-6x＜$\frac{1}{3}$-$\frac{x}{5}$，得x＞$\frac{7}{87}$；
∴适合这两个不等式的x值为$\frac{7}{87}$＜x$＜\frac{68}{27}$．
点评 本题考查了解一元一次不等式组：求解出两个不等式的解集，然后按照“同大取大，同小取小，大于小的小于大的取中间，小于小的大于大的无解”确定不等式组的解集．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
7．
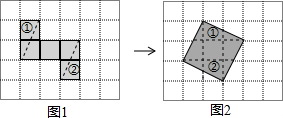如图1，每个小正方形的边长均为1，按虚线把阴影部分剪下来，用剪下来的阴影部分重新拼成如图2所示的正方形，那么所拼成的正方形的边长为（ ）
如图1，每个小正方形的边长均为1，按虚线把阴影部分剪下来，用剪下来的阴影部分重新拼成如图2所示的正方形，那么所拼成的正方形的边长为（ ）| A． | $\sqrt{5}$ | B． | 2 | C． | $\sqrt{3}$ | D． | $\sqrt{6}$ |
8．下列根式中，与$\sqrt{2}$是同类二次根式的是（ ）
| A． | $\sqrt{12}$ | B． | $\sqrt{8}$ | C． | $\sqrt{6}$ | D． | $\sqrt{5}$ |
12．如果点A（x-y，x+y）与点B（5，-3）关于y轴对称，那么x，y的值是（ ）
| A． | x=4，y=-1 | B． | x=-4，y=-1 | C． | x=4，y=1 | D． | x=-4，y=1 |
9．已知点P在第二象限，且P到x轴的距离为3，到y轴的距离为4，则P点的坐标为（ ）
| A． | （3，-4） | B． | （-3，4） | C． | （4，-3） | D． | （-4，3） |
如图，矩形ABCD中，AB=4，BC=6，P是CD边上的中点，E是BC边上的一动点，M，N分别是AE、PE的中点，则随着点E的运动，线段MN长的取值或取值范围为$\sqrt{10}$．