题目内容
13. 如图,AB∥CD,E、F分别在AB、CD上,若∠1+∠D=180°,那么EF与BD平行吗?为什么?
如图,AB∥CD,E、F分别在AB、CD上,若∠1+∠D=180°,那么EF与BD平行吗?为什么?
分析 由平行可知∠1+∠CFE=180°,结合条件可得∠CFE=∠D,可证明EF∥BD.
解答 解:EF∥BD,理有如下:
∵AB∥CD,
∴∠1+∠CFE=180°,
即∠CFE=180°-∠1,
∵∠1+∠D=180°,
∴∠D=180°-∠1,
∴∠CFE=∠D,
∴EF∥BD.
点评 本题主要考查平行线的判定和性质,掌握平行线的性质和判定是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
3.下列从左到右的变形是因式分解的是( )
| A. | (x-4)(x+4)=x2-16 | B. | x2-y2+2=(x+y)(x-y)+2 | ||
| C. | x2+1=x(x+$\frac{1}{x}$) | D. | a2b+ab2=ab(a+b) |
8.下列根式中,与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{8}$ | C. | $\sqrt{6}$ | D. | $\sqrt{5}$ |
18.下表中,y是x的一次函数,写出该函数表达式,并补全下表.
| x | -3 | -2 | -1 | 0 | 1 |
| y | 6 | 4 | 2 | 0 | -2 |
 如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC:∠EOD=2:3,∠BOD=36度.
如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC:∠EOD=2:3,∠BOD=36度.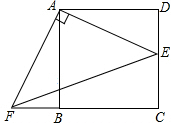 如图,已知点E是正方形ABCD边CD上的一点,点F在CB的延长线上,且DE=BF.求证:△AFE是等腰直角三角形.
如图,已知点E是正方形ABCD边CD上的一点,点F在CB的延长线上,且DE=BF.求证:△AFE是等腰直角三角形.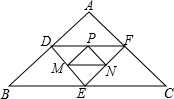 如图,点D、E、F分别是△ABC中AB、BC、AC边上的中点,点M、N、P分别是DE、EF、DF的中点.若△ABC的周长为24,则△PMN的周长为( )
如图,点D、E、F分别是△ABC中AB、BC、AC边上的中点,点M、N、P分别是DE、EF、DF的中点.若△ABC的周长为24,则△PMN的周长为( )