题目内容
18.已知|2a-5|+(4a-b-m)2=0,则当b>0时,求m的取值范围.分析 原式利用非负数的性质列出关系式,求出a的值,进而表示出b,代入b>0,即可求出m的范围.
解答 解:∵|2a-5|+(4a-b-m)2=0,
∴2a-5=0,4a-b-m=0,
解得:a=$\frac{5}{2}$,b=4a-m=10-m,
根据题意得:10-m>0,即m<10.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
8.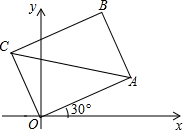 如图,矩形OABC的一顶点O恰好落在平面直角坐标系的坐标原点处,边OA与x轴正方向的夹角为30°.连结AC.若AB=6,AC=10,则点A的坐标为( )
如图,矩形OABC的一顶点O恰好落在平面直角坐标系的坐标原点处,边OA与x轴正方向的夹角为30°.连结AC.若AB=6,AC=10,则点A的坐标为( )
 如图,矩形OABC的一顶点O恰好落在平面直角坐标系的坐标原点处,边OA与x轴正方向的夹角为30°.连结AC.若AB=6,AC=10,则点A的坐标为( )
如图,矩形OABC的一顶点O恰好落在平面直角坐标系的坐标原点处,边OA与x轴正方向的夹角为30°.连结AC.若AB=6,AC=10,则点A的坐标为( )| A. | ($4\sqrt{3}$,4) | B. | (4,4) | C. | (4,$4\sqrt{3}$) | D. | (4,2) |
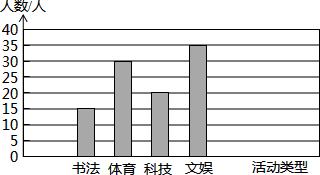 某校对初中学生开展的四项课外活动进行了一次抽样调查(每人只参加其中的一项活动),调查结果如图所示.根据图示所提供的样本数据,可得学生参加体育活动的频率是0.3.
某校对初中学生开展的四项课外活动进行了一次抽样调查(每人只参加其中的一项活动),调查结果如图所示.根据图示所提供的样本数据,可得学生参加体育活动的频率是0.3.